Feigenbaum Constant

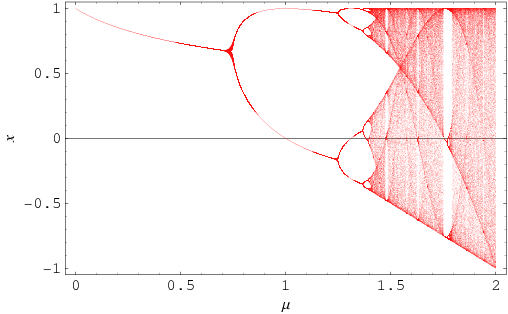
The Feigenbaum constant 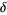 is a universal constant for functions approaching chaos via period doubling. It was discovered by Feigenbaum in 1975 (Feigenbaum 1979) while studying the fixed points of the iterated function

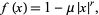(1)

and characterizes the geometric approach of the bifurcation parameter to its limiting value as the parameter 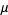 is increased for fixed . The plot above is made by iterating equation (1) with 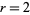 several hundred times for a series of discrete but closely spaced values of 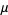, discarding the first hundred or so points before the iteration has settled down to its fixed points, and then plotting the points remaining.

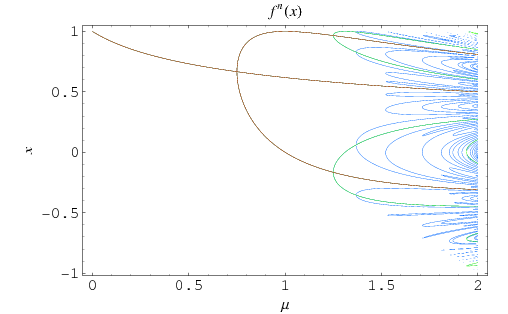
A similar plot that more directly shows the cycle may be constructed by plotting 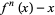 as a function of 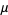. The plot above (Trott, pers. comm.) shows the resulting curves for 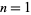, 2, and 4.

Let 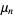 be the point at which a period 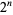-cycle appears, and denote the converged value by 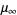. Assuming geometric convergence, the difference between this value and  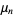is denoted

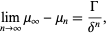(2)

where 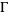 is a constant and  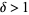is a constant now known as the Feigenbaum constant. Solving for  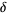gives

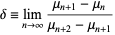(3)

(Rasband 1990, p. 23; Briggs 1991). An additional constant 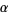, defined as the separation of adjacent elements of period doubled attractors from one double to the next, has a value

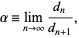(4)

where 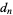 is the value of the nearest cycle element to 0 in the  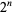cycle (Rasband 1990, p. 37; Briggs 1991).

For equation (1) with 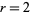, the onsets of bifurcations occur at 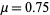, 1.25, 1.368099, 1.39405, 1.399631, ..., giving convergents to  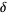for 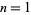, 2, 3, ... of 4.23374, 4.5515, 4.64617, ....

For the logistic map,

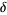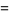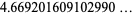			(5)
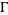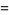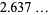			(6)
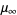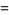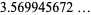			(7)
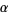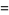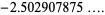			(8)

(OEIS A006890, A098587, and A006891; Broadhurst 1999; Wolfram 2002, p. 920), where 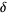 is known as the Feigenbaum constant and  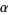is the associated "reduction parameter."

Briggs (1991) calculated 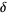 to 84 digits, Briggs (1997) to 576 decimal places (of which 344 were correct), and Broadhurst (1999) to 1018 decimal places. It is not known if the Feigenbaum constant  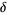is algebraic, or if it can be expressed in terms of other mathematical constants (Borwein and Bailey 2003, p. 53).

Briggs (1991) calculated 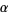 to 107 digits, Briggs (1997) to 576 decimal places (of which 346 were correct), and Broadhurst (1999) to 1018 decimal places.

Amazingly, the Feigenbaum constant 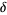 and associated reduction parameter  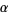are "universal" for all one-dimensional maps  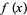if 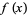 has a single locally quadratic maximum. This was conjecture by Feigenbaum, and demonstrated rigorously by Lanford (1982) for the case 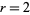, and by Epstein (1985) for all .

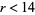More specifically, the Feigenbaum constant is universal for one-dimensional maps if the Schwarzian derivative

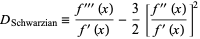(9)

is negative in the bounded interval (Tabor 1989, p. 220). Examples of maps which are universal include the Hénon map, logistic map, Lorenz attractor, Navier-Stokes truncations, and sine map 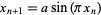. The value of the Feigenbaum constant can be computed explicitly using functional group renormalization theory. The universal constant also occurs in phase transitions in physics.

The value of 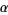 for a universal map may be approximated from functional group renormalization theory to the zeroth order by solving

(10)

which can be rewritten as the quintic equation

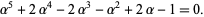(11)

Solving numerically for the smallest real root gives 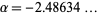, only 0.7% off from the actual value (Feigenbaum 1988).

For an area-preserving two-dimensional map with

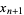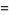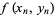			(12)
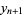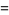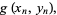			(13)

the Feigenbaum constant is 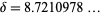 (Tabor 1989, p. 225).

For a function of the form (1), the Feigenbaum constant for various 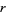 is given in the following table (Briggs 1991, Briggs et al. 1991, Finch 2003), which updates the values in Tabor (1989, p. 225).

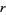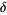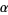3	5.9679687038...	1.9276909638...
4	7.2846862171...	1.6903029714...
5	8.3494991320...	1.5557712501...
6	9.2962468327...	1.4677424503...

Broadhurst (1999) considered additional Feigenbaum constants. Let 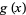 and 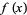 be even functions with  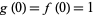and

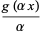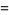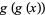			(14)
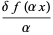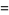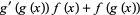			(15)

and 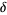 as large as possible. Let  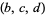be positive numbers with

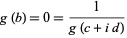(16)

and 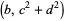 as small as possible. Also let  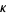be the order of the nearest singularity, with

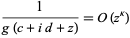(17)

as 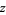 tends to zero. The values of these constants are summarized in the following table.

constant	OEIS	value
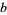	A119277	0.83236723690531642484...
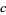	A119278	1.8312589849371314853...
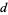	A119279	2.6831509004740718014...
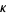	A119280	1.3554618047064087438...

REFERENCES:

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 53, 2003.

Briggs, K. "Simple Experiments in Chaotic Dynamics." Amer. J. Phys. 55, 1083-1089, 1987.

Briggs, K. "How to Calculate the Feigenbaum Constants on Your PC." Austral. Math. Soc. Gaz. 16, 89-92, 1989.

Briggs, K. "A Precise Calculation of the Feigenbaum Constants." Math. Comput. 57, 435-439, 1991.

Briggs, K. M. "Feigenbaum Scaling in Discrete Dynamical Systems." Ph.D. thesis. Melbourne, Australia: University of Melbourne, 1997.

Briggs, K.; Quispel, G.; and Thompson, C. "Feigenvalues for Mandelsets." J. Phys. A: Math. Gen. 24, 3363-3368, 1991.

Broadhurst, D. "Feigenbaum Constants to 1018 Decimal Places." Email dated 22-Mar-1999. http://pi.lacim.uqam.ca/piDATA/feigenbaum.txt.

Campanino, M. and Epstein, H. "On the Existence of Feigenbaum's Fixed Point." Commun. Math. Phys. 79, 261-302, 1981.

Campanino, M.; Epstein, H.; and Ruelle, D. "On Feigenbaum's Functional Equation." Topology 21, 125-129, 1982.

Collet, P. and Eckmann, J.-P. "Properties of Continuous Maps of the Interval to Itself." Mathematical Problems in Theoretical Physics (Ed. K. Osterwalder). New York: Springer-Verlag, 1979.

Collet, P. and Eckmann, J.-P. Iterated Maps on the Interval as Dynamical Systems. Boston, MA: Birkhäuser, 1980.

Derrida, B.; Gervois, A.; and Pomeau, Y. "Universal Metric Properties of Bifurcations." J. Phys. A 12, 269-296, 1979.

Eckmann, J.-P. and Wittwer, P. Computer Methods and Borel Summability Applied to Feigenbaum's Equations. New York: Springer-Verlag, 1985.

Epstein, H. "New Proofs of the Existence of the Feigenbaum Functions." Inst. Hautes Études Sco., Report No. IHES/P/85/55, 1985.

Feigenbaum, M. J. "The Universal Metric Properties of Nonlinear Transformations." J. Stat. Phys. 21, 669-706, 1979.

Feigenbaum, M. J. "The Metric Universal Properties of Period Doubling Bifurcations and the Spectrum for a Route to Turbulence." Ann. New York. Acad. Sci. 357, 330-336, 1980.

Feigenbaum, M. J. "Quantitative Universality for a Class of Non-Linear Transformations." J. Stat. Phys. 19, 25-52, 1978.

Feigenbaum, M. J. "Presentation Functions, Fixed Points, and a Theory of Scaling Function Dynamics." J. Stat. Phys. 52, 527-569, 1988.

Finch, S. R. "Feigenbaum-Coullet-Tresser Constants." §1.9 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 65-76, 2003.

Gleick, J. Chaos: Making a New Science. New York: Penguin Books, pp. 173-181, 1988.

Karamanos, K. and Kotsireas, I. "Addendum: On the Statistical Analysis of the First Digits of the Feigenbaum Constants." J. Franklin Inst. 343, 759-761, 2006.

Lanford, O. E. III. "A Computer-Assisted Proof of the Feigenbaum Conjectures." Bull. Amer. Math. Soc. 6, 427-434, 1982.

Lanford, O. E. III. "A Shorter Proof of the Existence of the Feigenbaum Fixed Point." Commun. Math. Phys. 96, 521-538, 1984.

Michon, G. P. "Final Answers: Numerical Constants." http://home.att.net/~numericana/answer/constants.htm#feigenbaum.

Pickover, C. A. "The Fifteen Most Famous Transcendental Numbers." J. Recr. Math. 25, 12, 1993.

Pickover, C. A. "The 15 Most Famous Transcendental Numbers." Ch. 44 in Wonders of Numbers, Adventures in Mathematics, Mind, and Meaning. Oxford, England: Oxford University Press, pp. 103-106, 2000.

Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, 1990.

Sloane, N. J. A. Sequences A006890/M3264, A006891/M1311, A098587, A119277, A119278, A119279, and A119280 in "The On-Line Encyclopedia of Integer Sequences."

Stephenson, J. W. and Wang, Y. "Numerical Solution of Feigenbaum's Equation." Appl. Math. Notes 15, 68-78, 1990.

Stephenson, J. W. and Wang, Y. "Relationships Between the Solutions of Feigenbaum's Equations." Appl. Math. Let. 4, 37-39, 1991.

Stoschek, E. "Modul 33: Algames with Numbers." http://marvin.sn.schule.de/~inftreff/modul33/task33.htm.

Thompson, C. J. and McGuire, J. B. "Asymptotic and Essentially Singular Solutions of the Feigenbaum Equation." J. Stat. Phys. 51, 991-1007, 1988.

Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989.

Trott, M. "The Mathematica Guidebooks Additional Material: Second Feigenbaum Constant." http://www.mathematicaguidebooks.org/additions.shtml#S_1_07.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 920, 2002.