Rule 30

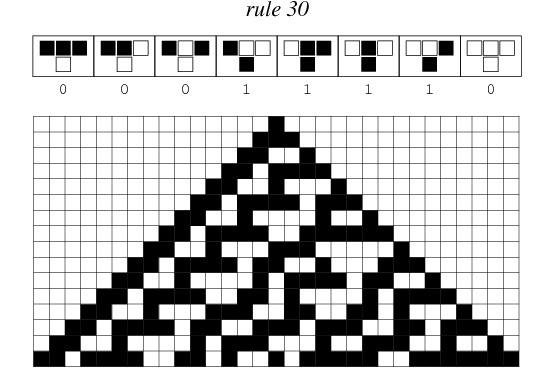
Rule 30 is one of the elementary cellular automaton rules introduced by Stephen Wolfram in 1983 (Wolfram 1983, 2002). It specifies the next color in a cell, depending on its color and its immediate neighbors. Its rule outcomes are encoded in the binary representation . This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (Wolfram 2002, p. 55).

250 iterations of rule 30 are illustrated above.

Starting with a single black cell, successive generations are given by interpreting the numbers 1, 7, 25, 111, 401, 1783, 6409, 28479, 102849, ... (OEIS A110240) in binary, namely 1, 111, 11001, 1101111, 110010001, ... (OEIS A070950).

Rule 30 is the mirror image, complement, and mirror complement of rules 86, 135, and 149, respectively.

Rule 30 is of special interest because it is chaotic (Wolfram 2002, p. 871), with central column given by 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, ... (OEIS A051023). In fact, this rule is used as the random number generator used for large integers in the Wolfram Language (Wolfram 2002, p. 317). Interpreting the central column as binary numbers and taking successive bits gives the sequence of numbers 1, 3, 6, 13, 27, 55, 110, 220, 441, 883, 1766, ... (OEIS A092539). The members of this sequence that are prime are 3, 13, 883, 237051898781, ... (OEIS A092540).

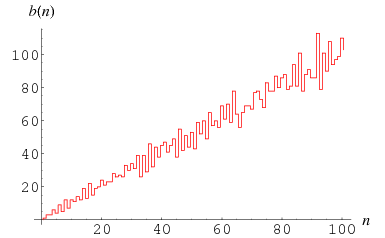
Jen (1990) proved that with the initial state of a single black cell, the sequence of colors attained in any two adjacent cells is not periodic (Gray 2003). The numbers of black cells 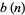 in consecutive generations 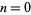, 1, ... are 1, 3, 3, 6, 4, 9, 5, 12, 7, ... (OEIS A070952), which is very closely fit by the line .

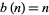The maximum runs of white cells at generations 0, 1, 2, ... are 0, 0, 2, 1, 3, 1, 4, 2, 5, 3, 4, 4, 3, 2, ... (OEIS A100053). The high-water marks are 0, 2, 3, 4, 5, 6, 8, 9, 11, 14, 15, 23, ... (OEIS A100054), which occur at positions 0, 2, 4, 6, 8, 16, 32, 43, 46, 64, 128, 256, 512, ... (OEIS A100055; Weisstein, Oct. 31, 2004) and look suspiciously like powers of 2 with a few additional values thrown in near the beginning.

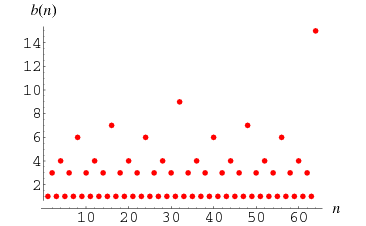
This result follows from the independent observation by E. Rowland (May 13, 2004) that the sequence of maximal black cells on the right side is 1, 3, 1, 4, 1, 3, 1, 6, 1, 3, 1, 4, 1, 3, 1, 7, 1, 3, 1, 4, ... (OEIS A094603), which have high water marks of 1, 3, 4, 6, 7, 9, 15, 16, 24, 25, 27, ... (OEIS A094604) at generations 0, 1, 3, 7, 15, ... (OEIS A000225; i.e., ).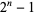

REFERENCES:

Gray, L. "A Mathematician Looks at Wolfram's New Kind of Science." Not. Amer. Math. Soc. 50, 200-211, 2003.

Jen, E. "Aperiodicity in One-Dimensional Cellular Automata." Physica D 45, 3-18, 1990.

Sloane, N. J. A. Sequences A000225/M2655, A051023, A070950, A070952, A092539, A092540, A094603, A094604, A100053, A100054, A100055, and A110240 in "The On-Line Encyclopedia of Integer Sequences."

Wolfram, S. "Statistical Mechanics of Cellular Automata." Rev. Mod. Phys. 55, 601-644, 1983.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 29-30, 52, 59, 317, and p. 871, 2002.