Topological Vector Space

A vector space with a T2-space topology such that the operations of vector addition and scalar multiplication are continuous. The interesting examples are infinite-dimensional spaces, such as a space of functions. For example, a Hilbert space and a Banach space are topological vector spaces.

The choice of topology reflects what is meant by convergence of functions. For instance, for functions whose integrals converge, the Banach space 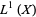, one of the L-p-spaces, is used. But if one is interested in pointwise convergence, then no norm will suffice. Instead, for each  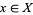define the seminorm

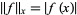on the vector space of functions on 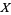. The seminorms define a topology, the smallest one in which the seminorms are continuous. So  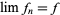is equivalent to  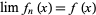for all 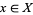, i.e., pointwise convergence. In a similar way, it is possible to define a topology for which "convergence" means uniform convergence on compact sets.

REFERENCES:

Köthe, G. Topological Vector Spaces. New York: Springer-Verlag, 1979.

Zimmer, R. Essential Results in Functional Analysis. Chicago: University of Chicago Press, pp. 13-17, 1990.