


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-8-2021
Date: 7-7-2021
Date: 10-6-2021
|
P. G. Tait undertook a study of knots in response to Kelvin's conjecture that the atoms were composed of knotted vortex tubes of ether (Thomson 1869). He categorized knots in terms of the number of crossings in a plane projection. He also made some conjectures which remained unproven until the discovery of Jones polynomials:
1. Reduced alternating diagrams have minimal link crossing number,
2. Any two reduced alternating diagrams of a given knot have equal writhe,
3. The flyping conjecture, which states that the number of crossings is the same for any reduced diagram of an alternating knot.
Conjectures (1) and (2) were proved by Kauffman (1987), Murasugi (1987ab), and Thistlethwaite (1987, 1988) using properties of the Jones polynomial or Kauffman polynomial F (Hoste et al. 1998). Conjecture (3) was proved true by Menasco and Thistlethwaite (1991, 1993) using properties of the Jones polynomial (Hoste et al. 1998).
REFERENCES:
Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First 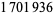 Knots." Math. Intell. 20, 33-48, Fall 1998.
Knots." Math. Intell. 20, 33-48, Fall 1998.
Kauffman, L. H. "State Models and the Jones Polynomial." Topology 26, 395-407, 1987.
Menasco, W. and Thistlethwaite, M. "The Tait Flyping Conjecture." Bull. Amer. Math. Soc. 25, 403-412, 1991.
Menasco, W. and Thistlethwaite, M. "The Classification of Alternating Links." Ann. Math. 138, 113-171, 1993.
Murasugi, K. "The Jones Polynomial and Classical COnjectures in Knot Theory." Topology 26, 187-194, 1987a.
Murasugi, K. "Jones Polynomials and Classical Conjectures in Knot Theory II." Math. Proc. Cambridge Philos. Soc. 102, 317-318, 1987b.
Tait, P. G. "On Knots I, II, III." Scientific Papers, Vol. 1. London: Cambridge University Press, pp. 273-347, 1900.
Thistlethwaite, M. B. "A Spanning Tree Expansion of the Jones Polynomial." Topology 26, 297-309, 1987.
Thistlethwaite, M. B. "Kauffman's Polynomial and Alternating Links." Topology 27, 311-318, 1988.
Thomson, W. H. "On Vortex Motion." Trans. Roy. Soc. Edinburgh 25, 217-260, 1869.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تعقد اجتماعها التحضيري لإقامة حفل التخرج المركزي لطلبة الجامعات العراقية
|
|
|