Row Space

The vector space generated by the rows of a matrix viewed as vectors. The row space of a 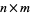 matrix  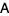with real entries is a subspace generated by  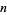elements of 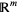, hence its dimension is at most equal to 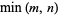. It is equal to the dimension of the column space of  (as will be shown below), and is called the rank of .

The row vectors of  are the coefficients of the unknowns 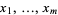 in the linear equation system

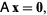(1)

where

(2)

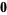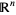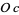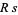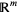and  is the zero vector in . Hence, the solutions span the orthogonal complement  to the row space  in , and

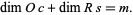(3)

On the other hand, the space of solutions also coincides with the kernel (or null space) of the linear transformation 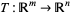, defined by

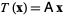(4)

for all vectors  of 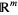. And it also true that

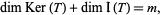(5)

where 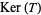 denotes the kernel and  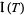the image, since the nullity and the rank always add up to the dimension of the domain. It follows that the dimension of the row space is

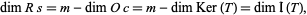(6)

which is equal to the dimension of the column space.