Borel Set

A Borel set is an element of a Borel sigma-algebra. Roughly speaking, Borel sets are the sets that can be constructed from open or closed sets by repeatedly taking countable unions and intersections. Formally, the class 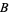 of Borel sets in Euclidean  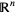is the smallest collection of sets that includes the open and closed sets such that if 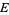, , 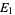, 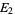... are in 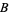, then so are 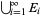, , 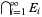and 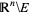, where  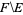is a set difference (Croft et al. 1991).

The set of rational numbers is a Borel set, as is the Cantor set.

REFERENCES:

Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 3, 1991.