المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر
أضيف حديثاً
غزوة الحديبية والهدنة بين النبي وقريش
2024-11-01
بعد الحديبية افتروا على النبي « صلى الله عليه وآله » أنه سحر
2024-11-01
المستغفرون بالاسحار
2024-11-01
المرابطة في انتظار الفرج
2024-11-01
النضوج الجنسي للماشية sexual maturity
2024-11-01
المخرجون من ديارهم في سبيل الله
2024-11-01

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
الباقلاء (الفول)
10-4-2016
تسع آيات إلى فرعون وقومه ! (1)
10-10-2014
البياض الدقيقي في الخرشوف
22-6-2016
فهم الذات
22-8-2022
لا إجماع إلاّ عن مستند
18-8-2016
جواز التيمم بغبار الثوب وغيره مع فقد الصعيد
25-12-2015

Chain Contraction  
  
1301   12:07 صباحاً   date: 6-5-2021
Author : Ranicki, A.
Book or Source : "Notes on Reidemeister Torsion." 1997. https://www.maths.ed.ac.uk/~aar/papers/torsion.pdf.
Page and Part : ...


Read More
Dense
Date: 18-7-2021 1695
Morse Theory
Date: 15-5-2021 1830
Borel Hierarchy
Date: 15-7-2021 1066

Chain Contraction

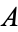Let A be a commutative ring, let 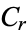C_r be an R-module for 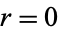r=0, 1, 2, ..., and define a chain complex 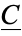C__ of the form

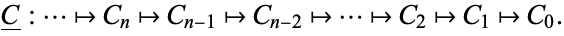C__:...|->C_n|->C_(n-1)|->C_(n-2)|->...|->C_2|->C_1|->C_0.

A chain contraction 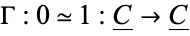Gamma:0=1:C__->C__ is a collection of R-modules morphisms 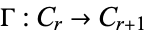Gamma:C_r->C_(r+1) such that, for all r>=0,

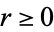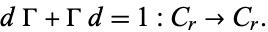dGamma+Gammad=1:C_r->C_r.

Here, 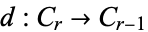d:C_r->C_(r-1) is the boundary map of C__.

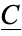REFERENCES:

Ranicki, A. "Notes on Reidemeister Torsion." 1997. https://www.maths.ed.ac.uk/~aar/papers/torsion.pdf.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
التاريخ / 2024-11-01

الأخبار العلمية
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
التاريخ / 2024-11-01

الساحة الاسلامية
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
التاريخ / 2024-10-31