


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-7-2021
Date: 27-5-2021
Date: 6-7-2021
|
The term Borel hierarchy is used to describe a collection of subsets of 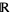 defined inductively as follows: Level one consists of all open and closed subsets of
defined inductively as follows: Level one consists of all open and closed subsets of 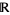 , and upon having defined levels
, and upon having defined levels 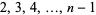 , level
, level 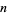 is obtained by taking countable unions and intersections of the previous level. In particular, level two of the hierarchy consists of the collections of all Fsigma and Gdelta sets while subsequent levels are described by way of the rather confusingly-named collection of sets of the form
is obtained by taking countable unions and intersections of the previous level. In particular, level two of the hierarchy consists of the collections of all Fsigma and Gdelta sets while subsequent levels are described by way of the rather confusingly-named collection of sets of the form 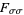 ,
, 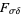 ,
, 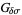 ,
, 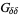 ,
, 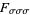 , etc.
, etc.
The collection of sets across all levels of the Borel hierarchy is the Borel sigma-algebra. As such, the Borel hierarchy is fundamental to the study of measure theory.
More general notions of the Borel hierarchy (and thus of Borel sets, etc.) are introduced and studied as part of various areas of set theory, topology, and mathematical logic.
REFERENCES:
Royden, H. L. and Fitzpatrick, P. M. Real Analysis. Pearson, 2010.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|