


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-6-2017
Date: 22-5-2021
Date: 5-8-2021
|
The Kauffman 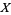 -polynomial, also called the normalized bracket polynomial, is a 1-variable knot polynomial denoted
-polynomial, also called the normalized bracket polynomial, is a 1-variable knot polynomial denoted 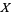 (Adams 1994, p. 153),
(Adams 1994, p. 153), 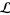 (Kauffman 1991, p. 33), or
(Kauffman 1991, p. 33), or 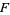 (Livingston 1993, p. 219), and defined for a link
(Livingston 1993, p. 219), and defined for a link 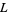 by
by
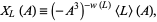 |
(1) |
where 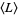 is the bracket polynomial and
is the bracket polynomial and 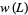 is the writhe of
is the writhe of 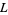 (Kauffman 1991, p. 33; Adams 1994, p. 153). It is implemented in the Wolfram Language as KnotData[knot, "BracketPolynomial"].
(Kauffman 1991, p. 33; Adams 1994, p. 153). It is implemented in the Wolfram Language as KnotData[knot, "BracketPolynomial"].
This polynomial is invariant under ambient isotopy, and relates mirror images by
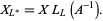 |
(2) |
It is identical to the Jones polynomial 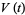 with the change of variable
with the change of variable
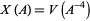 |
(3) |
and related to the two-variable Kauffman polynomial F by
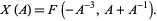 |
(4) |
The Kaufman 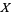 -polynomial of the trefoil knot is therefore
-polynomial of the trefoil knot is therefore
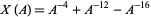 |
(5) |
(Kaufmann 1991, p. 35). The following table summarizes the polynomials for named knots.
| knot | Kaufman 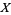 -polynomial -polynomial |
| figure eight knot | 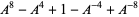 |
| Miller Institute knot | 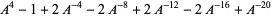 |
| Perko pair | 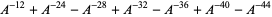 |
| Solomon's seal knot | 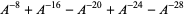 |
| stevedore's knot | 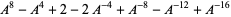 |
| trefoil knot | 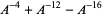 |
| unknot | 1 |
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, 1994.
Kauffman, L. H. Knots and Physics. Singapore: World Scientific, p. 33, 1991.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., 1993.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|