


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-6-2021
Date: 24-6-2017
Date: 29-7-2021
|
For a braid with 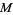 strands,
strands, 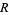 components,
components, 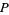 positive crossings, and
positive crossings, and 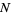 negative crossings,
negative crossings,
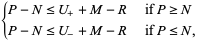 |
(1) |
where 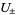 are the smallest number of positive and negative crossings which must be changed to crossings of the opposite sign. These inequalities imply Bennequin's conjecture. This inequality can also be extended to arbitrary knot diagrams.
are the smallest number of positive and negative crossings which must be changed to crossings of the opposite sign. These inequalities imply Bennequin's conjecture. This inequality can also be extended to arbitrary knot diagrams.
Menasco (1994) published a purported purely three-dimensional proof of the theorem that was discussed in Cipra (1994) and Menasco and Rudolph (1995). However, a hole in the proof was subsequently discovered by Otal. The hole has not yet been patched up, so the only proof of the inequality is the one due to Rudolph (1993), building on work by Kronheimer and Mrowka in four-dimensional topology.
REFERENCES:
Cipra, B. "From Knot to Unknot." What's Happening in the Mathematical Sciences, Vol. 2. Providence, RI: Amer. Math. Soc., pp. 8-13, 1994.
Kronheimer, P. B. and Mrowka, T. S. "Recurrence Relations and Asymptotics for Four-Manifold Invariants." Bull. Amer. Math. Soc. 30, 215-221, 1994.
Menasco, W. W. "The Bennequin-Milnor Unknotting Conjectures." C. R. Acad. Sci. Paris Sér. I Math. 318, 831-836, 1994.
Menasco, W. W. and Rudolph, L. "How Hard Is It to Untie a Knot?" Amer. Sci. 83, 38-49, 1995.
Rudolph, L. "Quasipositivity as an Obstruction to Sliceness." Bull. Amer. Math. Soc. 29, 51-59, 1993.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|