


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-6-2021
Date: 2-8-2021
Date: 11-5-2021
|
A characterization of normal spaces which states that a topological space 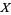 is normal iff, for any two nonempty closed disjoint subsets
is normal iff, for any two nonempty closed disjoint subsets 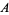 , and
, and 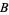 of
of 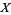 , there is a continuous map
, there is a continuous map ![f:X->[0,1]](https://mathworld.wolfram.com/images/equations/UrysohnsLemma/Inline5.gif) such that
such that 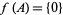 and
and 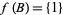 . A function
. A function 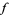 with this property is called a Urysohn function.
with this property is called a Urysohn function.
This formulation refers to the definition of normal space given by Kelley (1955, p. 112) or Willard (1970, p. 99). In the statement for an alternative definition (e.g., Cullen 1968, p. 118), the word "normal" has to be replaced by 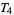 .
.
REFERENCES:
Cullen, H. F. Introduction to General Topology. Boston, MA: Heath, p. 124, 1968.
Joshi, K. D. "The Urysohn Characterization of Normality." §7.3 in Introduction to General Topology. New Delhi, India: Wiley, pp. 177-182, 1983.
Kelley, J. L. General Topology. New York: Van Nostrand Company, p. 115, 1955.
Willard, S. General Topology. Reading, MA: Addison-Wesley, p. 102, 1970.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|