Compact-Open Topology

The compact-open topology is a common topology used on function spaces. Suppose 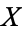 and 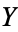 are topological spaces and  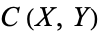is the set of continuous maps from 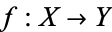. The compact-open topology on  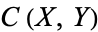is generated by subsets of the following form,

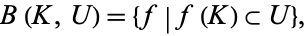(1)

where 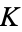 is compact in  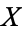and 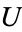 is open in 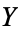. (Hence the terminology "compact-open.") It is important to note that these sets are not closed under intersection, and do not form a topological basis. Instead, the sets  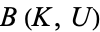form a subbasis for the compact-open topology. That is, the open sets in the compact-open topology are the arbitrary unions of finite intersections of .

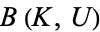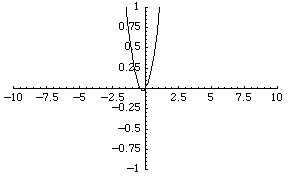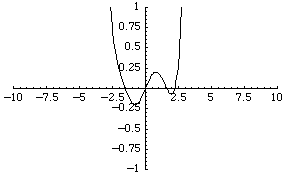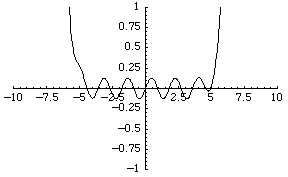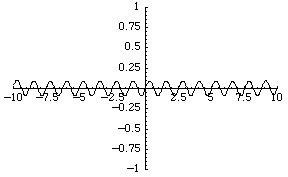
The simplest function space to compare topologies is the space of real-valued continuous functions 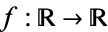. A sequence of functions  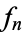converges to  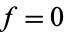iff for every  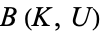containing  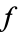contains all but a finite number of the 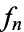. Hence, for all  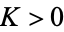and all 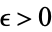, there exists an  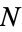such that for all ,

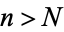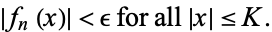(2)

For example, the sequence of functions 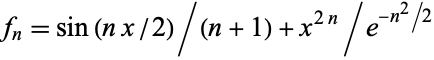 converges to the zero function, although each function is unbounded.

When 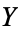 is a metric space, the compact-open topology is the same as the topology of compact convergence. If  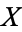is a locally compact T2-space, a fairly weak condition, then the evaluation map

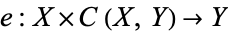(3)

defined by 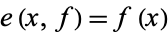 is continuous. Similarly,  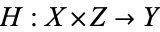is continuous iff the map 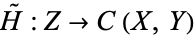, given by 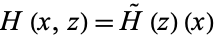, is continuous. Hence, the compact-open topology is the right topology to use in homotopy theory.