المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Lyapunov Condition |
 1661
 05:30 مساءً
date: 24-4-2021 |
Author : Ash, R. B. and Doléans-Dade, C. A. 
Book or Source : Probability & Measure Theory, 2nd ed. New York: Academic Press 
Page and Part : ...|
Read More
Date: 11-3-2021
1886
Date: 9-3-2021
1506
Date: 30-3-2021
1234
|
The Lyapunov condition, sometimes known as Lyapunov's central limit theorem, states that if the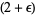 
th moment (with 
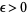) exists for a statistical distribution of independent random variates 
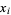(which need not necessarily be from same distribution), the means 
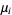and variances 
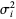are finite, and
 |
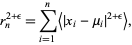(1) |
then if
 |
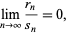(2) |
where
 |
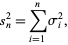(3) |
the central limit theorem holds.
REFERENCES:
Ash, R. B. and Doléans-Dade, C. A. Probability & Measure Theory, 2nd ed. New York: Academic Press, p. 307, 1999.
Billingsley, P. Probability and Measure, 2nd ed. New York: p. 371, Wiley, 1986.
Resnik, S. A Probability Path. Boston, MA: Birkhäuser, p. 319, 1999.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
