المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Lindeberg-Feller Central Limit Theorem |
 3419
 05:13 مساءً
date: 24-4-2021 |
Author : Feller, W. 
Book or Source : "Über den zentralen Genzwertsatz der Wahrscheinlichkeitsrechnung." Math. Z. 40 
Page and Part : ...|
Read More
Date: 4-4-2021
1846
Date: 18-4-2021
1871
Date: 8-2-2021
1471
|
If the random variates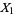 
, 
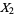, ... satisfy the Lindeberg condition, then for all 
,
 |
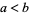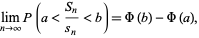where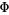 
is the normal distribution function.
REFERENCES:
Feller, W. "Über den zentralen Genzwertsatz der Wahrscheinlichkeitsrechnung." Math. Z. 40, 521-559, 1935.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, p. 229, 1968.
Lindeberg, J. W. "Eine neue Herleitung des Exponentialgesetzes in der Wahrschienlichkeitsrechnung." Math. Z. 15, 211-225, 1922.
Zabell, S. L. "Alan Turing and the Central Limit Theorem." Amer. Math. Monthly 102, 483-494, 1995.
|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|
