


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-4-2021
Date: 14-3-2021
Date: 19-4-2021
|
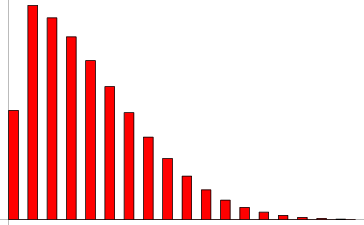
A fair coin is tossed an even 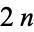 number of times. Let
number of times. Let 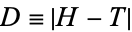 be the absolute difference in the number of heads and tails obtained. Then the probability distribution is given by
be the absolute difference in the number of heads and tails obtained. Then the probability distribution is given by
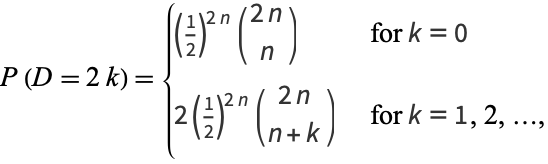 |
(1) |
where 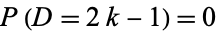 . The most probable value of
. The most probable value of 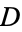 is
is 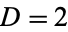 , and the expectation value is
, and the expectation value is
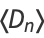 |
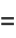 |
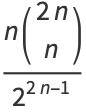 |
(2) |
 |
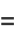 |
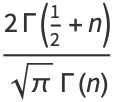 |
(3) |
 |
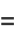 |
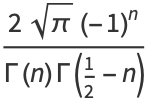 |
(4) |
 |
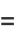 |
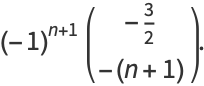 |
(5) |
The generating function for 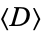 is given by
is given by
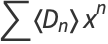 |
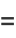 |
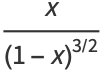 |
(6) |
 |
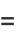 |
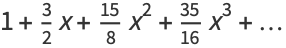 |
(7) |
(OEIS A001803 and A046161; Abramowitz and Stegun 1972, Prévost 1933; Hughes 1995). These numbers also arise in one-dimensional random walks.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 798, 1972.
Handelsman, M. B. Solution to Problem 436. "Distributing 'Heads' Minus 'Tails.' " College Math. J. 22, 444-446, 1991.
Hughes, B. D. Eq. (7.282) in Random Walks and Random Environments, Vol. 1: Random Walks. New York: Oxford University Press, p. 513, 1995.
Prévost, G. Tables de Fonctions Sphériques. Paris: Gauthier-Villars, pp. 156-157, 1933.
Sloane, N. J. A. Sequences A001803/M2986 and A046161 in "The On-Line Encyclopedia of Integer Sequences."a



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|