


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-2-2021
Date: 2-3-2021
Date: 19-4-2021
|
The discrete uniform distribution is also known as the "equally likely outcomes" distribution. Letting a set 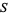 have
have 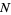 elements, each of them having the same probability, then
elements, each of them having the same probability, then
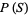 |
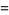 |
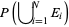 |
(1) |
 |
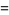 |
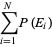 |
(2) |
 |
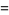 |
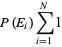 |
(3) |
 |
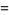 |
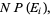 |
(4) |
so using 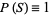 gives
gives
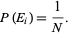 |
(5) |
Restricting the set 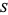 to the set of positive integers 1, 2, ...,
to the set of positive integers 1, 2, ..., 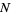 , the probability distribution function and cumulative distributions function for this discrete uniform distribution are therefore
, the probability distribution function and cumulative distributions function for this discrete uniform distribution are therefore
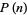 |
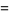 |
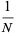 |
(6) |
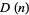 |
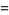 |
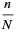 |
(7) |
for 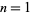 , ...,
, ..., 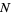 .
.
The discrete uniform distribution is implemented in the Wolfram Language as DiscreteUniformDistribution[n].
Its moment-generating function is
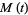 |
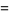 |
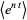 |
(8) |
 |
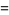 |
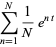 |
(9) |
 |
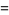 |
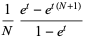 |
(10) |
 |
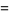 |
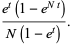 |
(11) |
The moments about 0 are
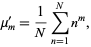 |
(12) |
so
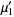 |
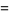 |
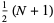 |
(13) |
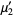 |
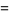 |
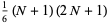 |
(14) |
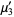 |
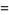 |
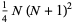 |
(15) |
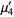 |
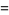 |
 |
(16) |
and the moments about the mean are
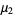 |
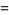 |
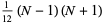 |
(17) |
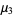 |
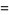 |
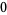 |
(18) |
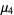 |
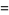 |
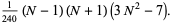 |
(19) |
The mean, variance, skewness, and kurtosis excess are
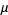 |
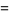 |
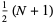 |
(20) |
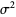 |
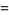 |
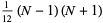 |
(21) |
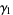 |
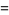 |
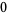 |
(22) |
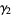 |
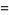 |
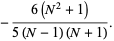 |
(23) |
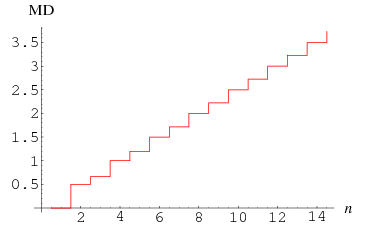
The mean deviation for a uniform distribution on 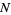 elements is given by
elements is given by
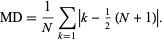 |
(24) |
To do the sum, consider separately the cases of 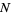 odd and
odd and 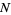 even. For
even. For 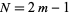 odd,
odd,
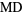 |
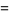 |
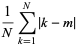 |
(25) |
 |
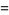 |
![1/N[sum_(k=1)^(m-1)m-k+sum_(k=m+1)^(N)k-m]](https://mathworld.wolfram.com/images/equations/DiscreteUniformDistribution/Inline80.gif) |
(26) |
 |
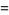 |
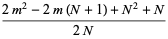 |
(27) |
 |
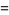 |
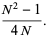 |
(28) |
Similarly, for 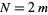 even,
even,
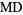 |
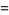 |
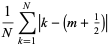 |
(29) |
 |
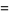 |
![1/N[sum_(k=1)^(m)(m+1/2)-k+sum_(k=m+1)^(N)k-(m+1/2)]](https://mathworld.wolfram.com/images/equations/DiscreteUniformDistribution/Inline93.gif) |
(30) |
 |
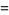 |
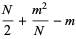 |
(31) |
 |
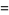 |
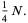 |
(32) |
The complete solution is therefore
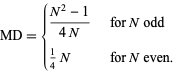 |
(33) |
For 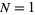 , 2, ..., the first few values are 0, 1/2, 2/3, 1, 6/5, 3/2, 12/7, ... (OEIS A086111 and A086112).
, 2, ..., the first few values are 0, 1/2, 2/3, 1, 6/5, 3/2, 12/7, ... (OEIS A086111 and A086112).
REFERENCES:
Sloane, N. J. A. Sequences A086111 and A086112 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|