


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات The score function 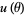 is the partial derivativeof the log-likelihood function
is the partial derivativeof the log-likelihood function 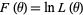 , where
, where 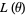 is the standard likelihood function.
is the standard likelihood function.
Defining the likelihood function
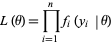 |
(1) |
shows that
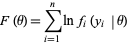 |
(2) |
and thus that
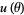 |
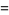 |
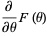 |
(3) |
 |
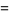 |
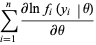 |
(4) |
 |
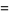 |
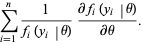 |
(5) |
Using the above formulation of 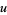 , one can easily compute various statistical measurements associated with
, one can easily compute various statistical measurements associated with 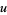 . For example, the mean
. For example, the mean 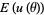 can be shown to equal zero while the variance is precisely the Fisher information matrix. The score function has extensive uses in many areas of mathematics, both pure and applied, and is a key component of the field of likelihood theory.
can be shown to equal zero while the variance is precisely the Fisher information matrix. The score function has extensive uses in many areas of mathematics, both pure and applied, and is a key component of the field of likelihood theory.
REFERENCES:
Rodriguez, G. "Lecture Notes on Generalized Linear Models." 2007. https://data.princeton.edu/wws509/notes/.
Sun, D. and Xiao, F. "Likelihood Theory with Score Function." 2013. https://www.stats.uwo.ca/faculty/bellhouse/Likelihood_Theory_with_Score_Function.pdf



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|