


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-10-2019
Date: 10-2-2020
Date: 30-6-2020
|
Let
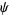 |
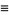 |
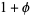 |
(1) |
 |
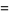 |
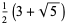 |
(2) |
 |
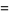 |
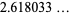 |
(3) |
(OEIS A104457), where 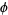 is the golden ratio, and
is the golden ratio, and
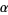 |
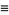 |
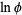 |
(4) |
 |
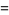 |
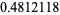 |
(5) |
(OEIS A002390).
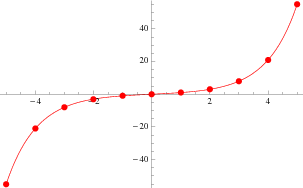
Define the Fibonacci hyperbolic sine by
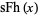 |
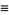 |
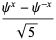 |
(6) |
 |
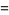 |
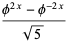 |
(7) |
 |
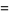 |
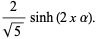 |
(8) |
The function satisfies
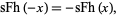 |
(9) |
and for 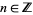 ,
,
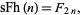 |
(10) |
where 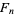 is a Fibonacci number. For
is a Fibonacci number. For 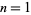 , 2, ..., the values are therefore 1, 3, 8, 21, 55, ... (OEIS A001906).
, 2, ..., the values are therefore 1, 3, 8, 21, 55, ... (OEIS A001906).
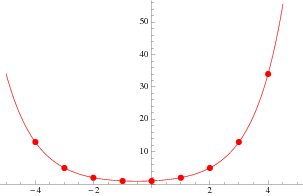
Define the Fibonacci hyperbolic cosine by
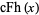 |
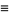 |
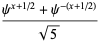 |
(11) |
 |
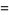 |
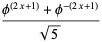 |
(12) |
 |
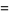 |
![2/(sqrt(5))cosh[(2x+1)alpha].](https://mathworld.wolfram.com/images/equations/FibonacciHyperbolicFunctions/Inline37.gif) |
(13) |
This function satisfies
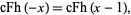 |
(14) |
and for 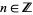 ,
,
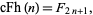 |
(15) |
where 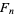 is a Fibonacci number. For
is a Fibonacci number. For 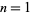 , 2, ..., the values are therefore 2, 5, 13, 34, 89, ... (OEIS A001519).
, 2, ..., the values are therefore 2, 5, 13, 34, 89, ... (OEIS A001519).
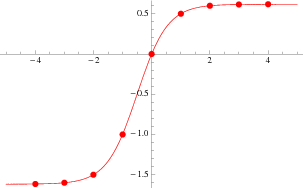
Similarly, the Fibonacci hyperbolic tangent is defined by
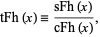 |
(16) |
and for 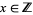 ,
,
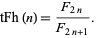 |
(17) |
For 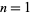 , 2, ..., the values are therefore 1/2, 3/5, 8/13, 21/34, 55/89, ... (OEIS A001906 and A001519).
, 2, ..., the values are therefore 1/2, 3/5, 8/13, 21/34, 55/89, ... (OEIS A001906 and A001519).
REFERENCES:
Sloane, N. J. A. Sequences A001519/M1439, A001906/M2741, A002390/M3318, and A104457 in "The On-Line Encyclopedia of Integer Sequences."
Stakhov, A. and Tkachenko, I. "Hyperbolic Fibonacci Trigonometry." Dokl. Akad. Nauk Ukrainy, No. 7, 9-14, 1993.
Trzaska, Z. W. "On Fibonacci Hyperbolic Trigonometry and Modified Numerical Triangles." Fib. Quart. 34, 129-138, 1996.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|