Mertens Conjecture

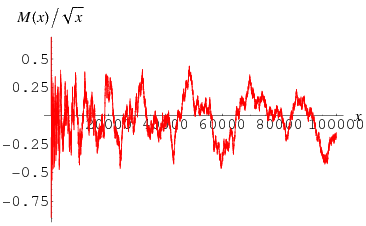
Given the Mertens function defined by

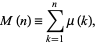(1)

where 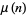 is the Möbius function, Stieltjes claimed in an 1885 letter to Hermite that  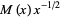stays within two fixed bounds, which he suggested could probably be taken to be  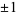(Havil 2003, p. 208). In the same year, Stieltjes (1885) claimed that he had a proof of the general result. However, it seems likely that Stieltjes was mistaken in this claim (Derbyshire 2004, pp. 160-161). Mertens (1897) subsequently published a paper opining based on a calculation of  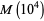that Stieltjes' claim

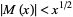(2)

for 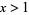 was "very probable."

The Mertens conjecture has important implications, since the truth of any equality of the form

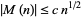(3)

for any fixed 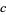 (the form of the Mertens conjecture with 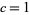) would imply the Riemann hypothesis. In fact, the statement

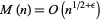(4)

for any 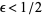 is equivalent to the Riemann hypothesis (Derbyshire 2004, p. 251).

Mertens (1897) verified the conjecture for 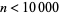, and this was subsequently extended to  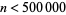by von Sterneck (1912; Deléglise and Rivat 1996). The Mertens conjecture was proved false by Odlyzko and te Riele (1985). Their proof is indirect and does not produce a specific counterexample, but it does show that

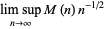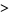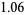			(5)
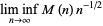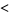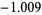			(6)

(Havil 2003, p. 209). Odlyzko and te Riele (1985) believe that there are no counterexamples to the Mertens conjecture for 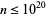, or even 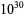, calling Stieltjes' supposed proof into very strong question (Derbyshire 2004, p. 161).

Pintz (1987) subsequently showed that at least one counterexample to the conjecture occurs for 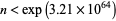 (Havil 2003, p. 209), using a weighted integral average of  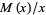and a discrete sum involving nontrivial zeros of the Riemann zeta function. The first value of  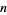for which  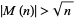is still unknown, but it is known to exceed  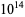(te Riele 2006), improving the previous best results of  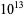(Lioen and van de Lune 1994) and  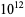(Dress 1993; Deléglise and Rivat 1996).

It is still not known if

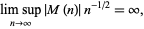(7)

although it seems very probable (Odlyzko and te Riele 1985).

REFERENCES:

Anderson, R. J. "On the Mertens Conjecture for Cusp Forms." Mathematika 26, 236-249, 1979.

Anderson, R. J. "Corrigendum: 'On the Mertens Conjecture for Cusp Forms.' " Mathematika 27, 261, 1980.

Deléglise, M. and Rivat, J. "Computing the Summation of the Möbius Function." Experiment. Math. 5, 291-295, 1996.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Devlin, K. "The Mertens Conjecture." Irish Math. Soc. Bull. 17, 29-43, 1986.

Dress, F. "Fonction sommatoire de la fonction de Möbius; 1. Majorations expérimentales." Experiment. Math. 2, 93-102, 1993.

Grupp, F. "On the Mertens Conjecture for Cusp Forms." Mathematika 29, 213-226, 1982.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 64, 1999.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Jurkat, W. and Peyerimhoff, A. "A Constructive Approach to Kronecker Approximation and Its Application to the Mertens Conjecture." J. reine angew. Math. 286/287, 322-340, 1976.

Lehman, R. S. "On Liouville's Functions." Math. Comput. 14, 311-320, 1960.

Lioen, W. M. and van de Lune, J. "Systematic Computations on Mertens' Conjecture and Dirichlet's Divisor Problem by Vectorized Sieving." In From Universal Morphisms to Megabytes: A Baayen Space Odyssey. On the Occasion of the Retirement of P. C. Baayen (Ed. K. Apt, L. Schrijver, and N. Temme). Amsterdam, Netherlands: Stichting Mathematisch Centrum, Centrum voor Wiskunde en Informatica, pp. 421-432, 1994. https://walter.lioen.com/papers/LL94.pdf.

Mertens, F. "Über eine zahlentheoretische Funktion." Sitzungsber. Akad. Wiss. Wien IIa 106, 761-830, 1897.

Odlyzko, A. M. and te Riele, H. J. J. "Disproof of the Mertens Conjecture." J. reine angew. Math. 357, 138-160, 1985.

Pintz, J. "An Effective Disproof of the Mertens Conjecture." Astérique 147-148, 325-333 and 346, 1987.

Stieltjes, T. C. R. A. S. 1885.

te Riele, H. J. J. "Some Historical and Other Notes About the Mertens Conjecture and Its Recent Disproof." Nieuw Arch. Wisk. 3, 237-243, 1985.

te Riele, H. R. "The Mertens Conjecture Revisited." 7th Algorithmic Number Theory Symposium. Technische Universität Berlin, 23-28 July 2006. https://www.math.tu-berlin.de/~kant/ants/Proceedings/te_riele/te_riele_talk.pdf.

von Sterneck, R. D. "Die zahlentheoretische Funktion 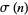 bis zur Grenze 500000." Akad. Wiss. Wien Math.-Natur. Kl. Sitzungsber. IIa 121, 1083-1096, 1912.