


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2020
Date: 1-11-2019
Date: 31-10-2019
|
There exists a positive integer 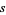 such that every sufficiently large integer is the sum of at most
such that every sufficiently large integer is the sum of at most 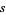 primes. It follows that there exists a positive integer
primes. It follows that there exists a positive integer 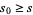 such that every integer
such that every integer 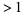 is a sum of at most
is a sum of at most 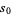 primes. The smallest proven value of
primes. The smallest proven value of 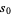 is known as the Schnirelmann constant.
is known as the Schnirelmann constant.
Schnirelmann's theorem can be proved using Mann's theorem, although Schnirelmann used the weaker inequality
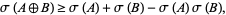 |
where 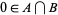 ,
, 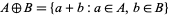 , and
, and 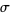 is the Schnirelmann density. Let
is the Schnirelmann density. Let 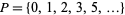 be the set of primes, together with 0 and 1, and let
be the set of primes, together with 0 and 1, and let 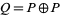 . Using a sophisticated version of the inclusion-exclusion principle, Schnirelmann showed that although
. Using a sophisticated version of the inclusion-exclusion principle, Schnirelmann showed that although 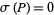 ,
, 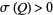 . By repeated applications of Mann's theorem, the sum of
. By repeated applications of Mann's theorem, the sum of 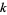 copies of
copies of 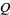 satisfies
satisfies 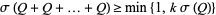 . Thus, if
. Thus, if 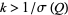 , the sum of
, the sum of 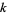 copies of
copies of 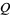 has Schnirelmann density 1, and so contains all positive integers.
has Schnirelmann density 1, and so contains all positive integers.
REFERENCES:
Khinchin, A. Y. "The Landau-Schnirelmann Hypothesis and Mann's Theorem." Ch. 2 in Three Pearls of Number Theory. New York: Dover, pp. 18-36, 1998.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|