


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-9-2020
Date: 4-7-2020
Date: 10-9-2020
|
Find two distinct sets of integers 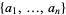 and
and 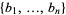 , such that for
, such that for 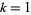 , ...,
, ..., 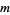 ,
,
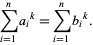 |
(1) |
The Prouhet-Tarry-Escott problem is therefore a special case of a multigrade equation. Solutions with 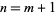 are said to be "ideal" and are of interest because they are minimal solutions of the problem (Borwein and Ingalls 1994).
are said to be "ideal" and are of interest because they are minimal solutions of the problem (Borwein and Ingalls 1994).
The smallest symmetric ideal solutions for 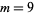 was found by Borwein et al. (Lisonek 2000),
was found by Borwein et al. (Lisonek 2000),
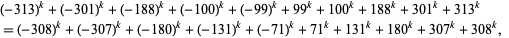 |
(2) |
as well as the second solution
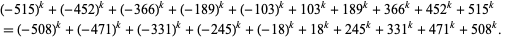 |
(3) |
The previous smallest known symmetric ideal solution, found by Letac in the 1940s, is
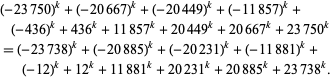 |
(4) |
In 1999, S. Chen found the first ideal solution with 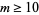 ,
,
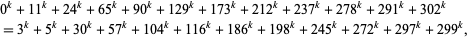 |
(5) |
which is true for 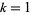 , 2, ..., 11.
, 2, ..., 11.
REFERENCES:
Borwein, P. and Ingalls, C. "The Prouhet-Tarry-Escott Problem Revisited." Enseign. Math. 40, 3-27, 1994. https://www.cecm.sfu.ca/~pborwein/PAPERS/P98.ps.
Chen, S. "The Prouhet-Tarry-Escott Problem." https://member.netease.com/~chin/eslp/TarryPrb.htm.
Chernick, J. "Ideal Solutions of the Tarry-Escott Problem." Amer. Math. Monthly 44, 62600633, 1937.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, pp. 709-710, 2005.
Dorwart, H. L. and Brown, O. E. "The Tarry-Escott Problem." Amer. Math. Monthly 44, 613-626, 1937.
Hahn, L. "The Tarry-Escott Problem." Problem 10284. Amer. Math. Monthly 102, 843-844, 1995.
Hardy, G. H. and Wright, E. M. "The Four-Square Theorem" and "The Problem of Prouhet and Tarry: The Number 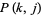 ." §20.5 and 21.9 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 302-306 and 328-329, 1979.
." §20.5 and 21.9 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 302-306 and 328-329, 1979.
Lisonek, P. "New Size 10 Solutions of the Prouhet-Tarry-Escott Problem." 21 Jun 2000. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0006&L=nmbrthry&P=558.
Shuwen, C. "Equal Sums of Like Powers." https://euler.free.fr/eslp/h12468.htm.
Sinha, T. "On the Tarry-Escott Problem." Amer. Math. Monthly 73, 280-285, 1966.
Sinha, T. "Some System of Diophantine Equations of the Tarry-Escott Type." J. Indian Math. Soc. 30, 15-25, 1966.
Wright, E. M. "On Tarry's Problem (I)." Quart. J. Math. Oxford Ser. 6, 216-267, 1935.
Wright, E. M. "The Tarry-Escott and the 'Easier' Waring Problem." J. reine angew. Math. 311/312, 170-173, 1972.
Wright, E. M. "Prouhet's 1851 Solution of the Tarry-Escott Problem of 1910." Amer. Math. Monthly 102, 199-210, 1959.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|