Composite Number

A composite number 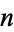 is a positive integer  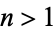which is not prime (i.e., which has factors other than 1 and itself). The first few composite numbers (sometimes called "composites" for short) are 4, 6, 8, 9, 10, 12, 14, 15, 16, ... (OEIS A002808), whose prime decompositions are summarized in the following table. Note that the number 1 is a special case which is considered to be neither composite nor prime.

	prime factorization		prime factorization
4		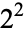20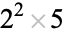
6		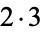21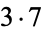
8		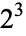22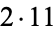
9		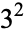24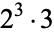
10		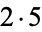25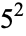
12		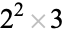26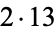
14		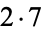27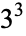
15		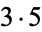28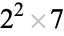
16		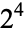30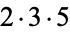
18		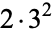32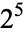

The 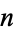th composite number  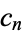can be generated using the Wolfram Language code

  Composite[n_Integer] :=
    FixedPoint[n + PrimePi[#] + 1&, n]

The Dirichlet generating function of the characteristic function of the composite numbers 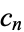 is given by

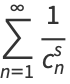			(1)
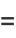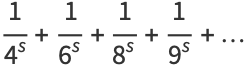			(2)
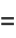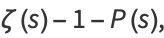			(3)

where 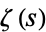 is the Riemann zeta function,  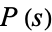is the prime zeta function, and  is an Iverson bracket.

There are an infinite number of composite numbers.

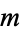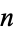The composite number problem asks if there exist positive integers  and  such that .

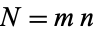A composite number 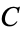 can always be written as a product in at least two ways (since  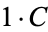is always possible). Call these two products

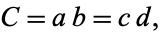(4)

then it is obviously the case that 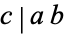 ( 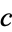divides 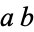). Set

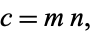(5)

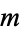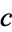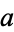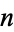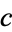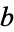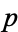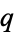where  is the part of  which divides , and  is the part of  which divides . Then there are  and  such that

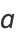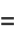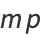			(6)
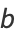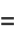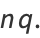			(7)

Solving 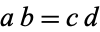 for 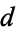 gives

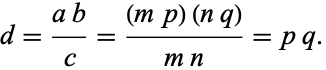(8)

It then follows that

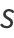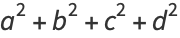			(9)
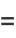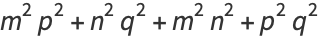			(10)
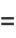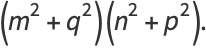			(11)

It therefore follows that 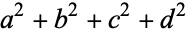 is never prime! In fact, the more general result that

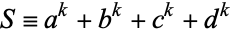(12)

is never prime for 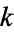 an integer  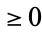also holds (Honsberger 1991).

REFERENCES:

Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 19-20, 1991.

Sloane, N. J. A. Sequence A002808/M3272 in "The On-Line Encyclopedia of Integer Sequences."