Frey Curve

Let 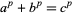 be a solution to Fermat's last theorem. Then the corresponding Frey curve is

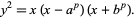(1)

Ribet (1990a) showed that such curves cannot be modular, so if the Taniyama-Shimura conjecture were true, Frey curves couldn't exist and Fermat's last theorem would follow with 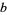 even and 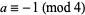. Frey curves are semistable. Invariants include the elliptic discriminant

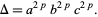(2)

The minimal discriminant is

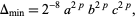(3)

the j-conductor is

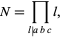(4)

and the j-invariant is

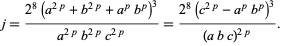(5)

REFERENCES:

Cox, D. A. "Introduction to Fermat's Last Theorem." Amer. Math. Monthly 101, 3-14, 1994.

Gouvêa, F. Q. "A Marvelous Proof." Amer. Math. Monthly 101, 203-222, 1994.

Ribet, K. A. "From the Taniyama-Shimura Conjecture to Fermat's Last Theorem." Ann. Fac. Sci. Toulouse Math. 11, 116-139, 1990a.

Ribet, K. A. "On Modular Representations of 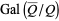 Arising from Modular Forms." Invent. Math. 100, 431-476, 1990b.