


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-6-2019
Date: 27-8-2019
Date: 3-6-2019
|
![sum_(n=0)^infty(H_n(x)H_n(y))/(n!)(1/2w)^n=(1-w^2)^(-1/2)exp[(2xyw-(x^2+y^2)w^2)/(1-w^2)],](http://mathworld.wolfram.com/images/equations/MehlersHermitePolynomialFormula/NumberedEquation1.gif) |
(1) |
where 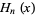 is a Hermite polynomial (Watson 1933; Erdélyi 1938; Szegö 1975, p. 380). The generating function
is a Hermite polynomial (Watson 1933; Erdélyi 1938; Szegö 1975, p. 380). The generating function
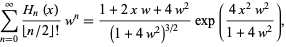 |
(2) |
where 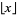 is the floor function, can be derived from this equation (Doetsch 1930; Szegö 1975, p. 380). The more straightforward sum with
is the floor function, can be derived from this equation (Doetsch 1930; Szegö 1975, p. 380). The more straightforward sum with 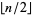 replaced by
replaced by 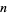 in the denominator is given by
in the denominator is given by
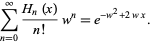 |
(3) |
REFERENCES:
Almqvist, G. and Zeilberger, D. "The Method of Differentiating Under the Integral Sign." J. Symb. Comput. 10, 571-591, 1990.
Doetsch, G. "Integralgleichenschaften der Hermiteschen Polynome." Math. Z. 32, 587-599, 1930.
Erdélyi, A. "Über eine erzeugende Funktion von Produkten Hermitescher Polynome." Math. Z. 44, 201-211, 1938.
Foata, D. "A Combinatorial Proof of the Mehler Formula." J. Comb. Th. Ser. A 24, 250-259, 1978.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, pp. 194-195, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Rainville, E. D. Special Functions. New York: Chelsea, p. 198, 1971.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., p. 380, 1975.
Watson, G. N. "Notes on Generating Functions of Polynomials: (2) Hermite Polynomials." J. London Math. Soc. 8, 194-199, 1933.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|