


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-3-2019
Date: 30-6-2019
Date: 16-5-2018
|
The first few values of 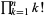 (known as a superfactorial) for
(known as a superfactorial) for 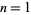 , 2, ... are given by 1, 2, 12, 288, 34560, 24883200, ... (OEIS A000178).
, 2, ... are given by 1, 2, 12, 288, 34560, 24883200, ... (OEIS A000178).
The first few positive integers that can be written as a product of factorials are 1, 2, 4, 6, 8, 12, 16, 24, 32, 36, 48, 64, 72, ... (OEIS A001013).
The number of ways that 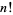 is a product of smaller factorials, each greater than 1, for
is a product of smaller factorials, each greater than 1, for 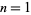 , 2, ... is given by 0, 0, 0, 1, 0, 1, 0, 1, 1, 2, 0, ... (OEIS A034876), and the numbers of products of factorials not exceeding
, 2, ... is given by 0, 0, 0, 1, 0, 1, 0, 1, 1, 2, 0, ... (OEIS A034876), and the numbers of products of factorials not exceeding 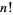 are 1, 2, 4, 8, 15, 28, 49, 83, ... (OEIS A101976).
are 1, 2, 4, 8, 15, 28, 49, 83, ... (OEIS A101976).
The only known factorials which are products of factorials in an arithmetic progression of three or more terms are
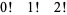 |
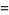 |
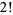 |
(1) |
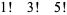 |
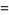 |
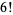 |
(2) |
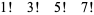 |
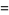 |
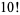 |
(3) |
(Madachy 1979).
The only solutions to
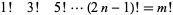 |
(4) |
are
 |
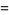 |
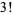 |
(5) |
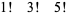 |
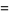 |
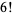 |
(6) |
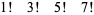 |
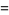 |
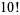 |
(7) |
(Cucurezeanu and Enkers 1987).
There are no nontrivial identities of the form
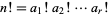 |
(8) |
for 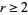 with
with 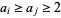 for
for 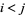 for
for 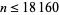 except
except
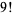 |
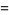 |
 |
(9) |
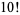 |
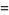 |
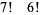 |
(10) |
 |
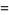 |
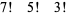 |
(11) |
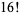 |
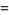 |
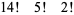 |
(12) |
(Madachy 1979; Guy 1994, p. 80). Here, "nontrivial" means that identities with 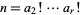 , or equivalently
, or equivalently 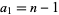 are excluded, since there are many identities of this form, e.g.,
are excluded, since there are many identities of this form, e.g., 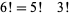 .
.
Values of 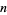 for which
for which 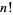 can be written as a product of smaller factorials are 1, 4, 6, 8, 9, 10, 12, 16, 24, ... (OEIS A034878).
can be written as a product of smaller factorials are 1, 4, 6, 8, 9, 10, 12, 16, 24, ... (OEIS A034878).
REFERENCES:
Cucurezeanu, I. and Enkers, D. "Problem E3063." Amer. Math. Monthly 94, 190, 1987.
Guy, R. K. "Equal Products of Factorials," "Alternating Sums of Factorials," and "Equations Involving Factorial 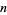 ." §B23, B43, and D25 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 80, 100, and 193-194, 1994.
." §B23, B43, and D25 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 80, 100, and 193-194, 1994.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 174, 1979.
Sloane, N. J. A. Sequences A000178/M2049, A001013/M0993, A034876, A034878, and A101976 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|