
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-5-2019
Date: 25-5-2019
Date: 25-9-2019
|
The elliptic exponential function 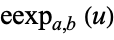 gives the value of
gives the value of 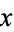 in the elliptic logarithm
in the elliptic logarithm
 |
for 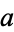 and
and 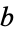 real such that
real such that 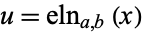 .
.
It is implemented in the Wolfram Language as EllipticExp[u,  a, b
a, b ], which returns
], which returns 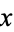 together with the superfluous parameter
together with the superfluous parameter 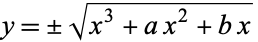 which multiplies the above integral by a factor of
which multiplies the above integral by a factor of 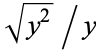 .
.
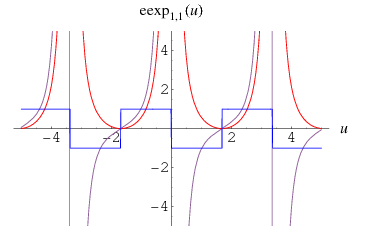
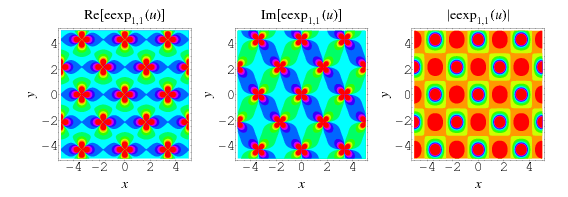
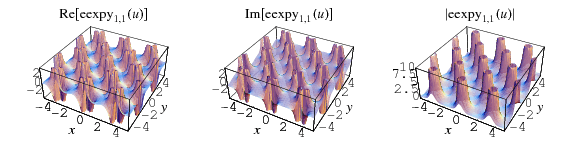
The top plot above shows 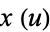 (red),
(red), 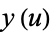 (violet), and
(violet), and 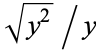 (blue) for
(blue) for  . The other plots show
. The other plots show  in the complex plane.
in the complex plane.
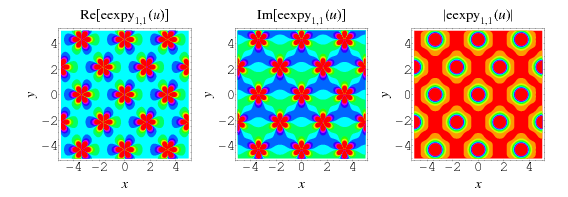
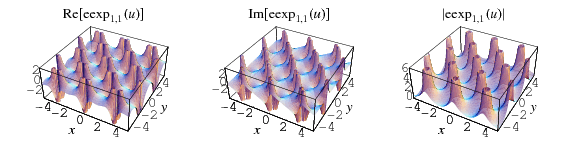
The plots above show 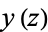 in the complex plane for
in the complex plane for 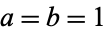 .
.
As can be seen from the plots, the elliptic exponential function is doubly periodic in the complex plane.
REFERENCES:
Wolfram, S. The Mathematica Book, 5th ed. Champaign, IL: Wolfram Media, p. 788, 2003.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|