المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Polynomial Height |
 947
 03:22 مساءً
date: 13-2-2019 |
Author : Zippel, R 
Book or Source : "Heights of Polynomials." §11.1 in Effective Polynomial Computation. Boston, MA: Kluwer 
Page and Part : pp. 174-175|
Read More
Date: 21-1-2019
1450
Date: 23-2-2019
935
Date: 21-1-2019
867
|
The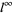 
-polynomial norm defined for a polynomial 
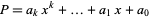by
 |
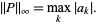Note that some authors (especially in the area of Diophantine analysis) use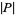 
as a shorthand for 
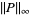, while others (especially in the area of computational complexity) used 
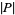to denote the 
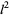-norm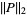 
(Zippel 1993, p. 174).
REFERENCES:
Zippel, R. "Heights of Polynomials." §11.1 in Effective Polynomial Computation. Boston, MA: Kluwer, pp. 174-175, 1993.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|
