Sendov Conjecture

The Sendov conjecture, proposed by Blagovest Sendov circa 1958, that for a polynomial 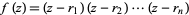 with 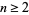 and each root  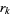located inside the closed unit disk  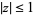in the complex plane, it must be the case that every closed disk of radius 1 centered at a root  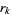will contain a critical point of 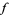. Since the Lucas-Gauss theorem implies that the critical points (i.e., the roots of the derivative) of  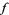must themselves lie in the unit disk, it seems completely implausible that the conjecture could be false. Yet at present it has not been proved even for polynomials with real coefficients, nor for any polynomials whose degree exceeds eight.

REFERENCES:

Rahman, Q. I. and Schmeisser, G. Analytic Theory of Polynomials. Oxford, England: Oxford University Press, 2002.

Schmeisser, G. "The Conjectures of Sendov and Smale." In Approximation Theory: A Volume Dedicated to Blagovest Sendov(Ed. B. Bojoanov). Sofia, Bulgaria: DARBA, pp. 353-369, 2002.