Green's Function--Poisson's Equation

Poisson's equation is

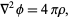(1)

where 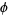 is often called a potential function and  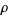a density function, so the differential operator in this case is 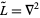. As usual, we are looking for a Green's function  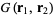such that

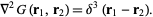(2)

But from Laplacian,

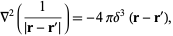(3)

so

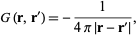(4)

and the solution is

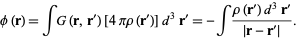(5)

Expanding 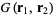 in the spherical harmonic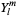s  gives

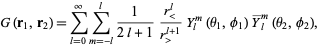(6)

where  and 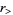 are greater than/less than symbols. this expression simplifies to

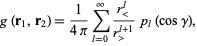(7)

where 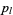 are Legendre polynomials, and 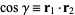. Equations (6) and (7) give the addition theorem for Legendre polynomials.

In cylindrical coordinates, the Green's function is much more complicated,

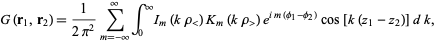(8)

where 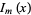 and 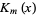 are modified Bessel functions of the first and second kinds (Arfken 1985).

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 485-486, 905, and 912, 1985.