مثال 3–4 (كتلة تنزلق أفقيا باحتكاك). تنزلق كتلة m على سطح أفقي. معامل الاحتكاك الحركي بين الكتلة والسطح هو μ_k. إذا كان مقدار السرعة الابتدائية هو v₀، فما المسافة التي تتحركها الكتلة قبل أن تصبح ساكنة؟ وما مقدار الزمن الذي تستغرقه الكتلة قبل أن تسكن؟

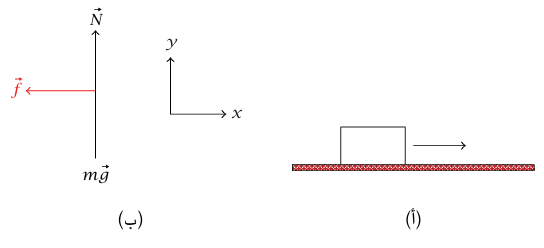
شكل 3–4: رسم توضيحي (أ) ومخطط الجسم الحر (ب) للمثال 3–4.

هذه المسألة البسيطة جدًّا تشتمل على كلٌّ من الكينماتيكا والديناميكا. ويفضل الأساتذة أن يضعوا هذا النوع من المسائل كامتحان؛ لأنه يختبر معرفة الطالب في المجالين، ويختبر أيضًا ما إذا كان قد دمج المعرفة في صورة قابلة للاستعمال. الديناميكا (أي 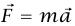) مطلوبة لحساب العجلة التناقصية للكتلة؛ وما إن تُعرف هذه العجلة التناقصية، فإنه يمكن حساب المسافة والزمن من الصيغ الكينماتيكية.

نفترض أن الكتلة تحركت إلى اليمين، ونضع المحورين x وy كما في شكل 3–3 (ب). العجلة 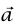 خالصة في الاتجاه x؛ أي إن a_x = a، و0a_y =  (نتوقع أن تكون a سالبة) القوى المؤثرة على الكتلة (شكل 3–3) هي: القوة التثاقلية، والقوة العمودية  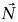التي يبذلها السطح، وقوة الاحتكاك  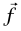التي يبذلها السطح. بكتابة  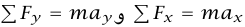نجد أن f = ma– و0 = N – mg. بتذكُّر أن f = μ_k N، نجد أن f = μ_k mg وبهذا تكون μ_k g–f/m = –.a =  المسافة المقطوعة D في الإيقاف يمكن إيجادها بسهولة أكثر من المعادلة (d11–1) التي تعطي  الزمن T اللازم للإيقاف يمكن إيجاده بسهولة أكثر من المعادلة (a11–1) التي تعطي

نطبق الآن منهجية نيوتن لتحليل «آلة أتوود» (شكل 3–5 (أ)) التي تتكون ببساطة من كتلتين ₁m وm₂ متصلتين بوتر (خيط) يمر فوق بكرة، تُستخدم دعامة للإبقاء على موضع مركز البكرة ثابتًا (مثلا، الحامل في شكل 3–5 (أ)) . احسب العجلة لكل كتلة والشد في الوتر.

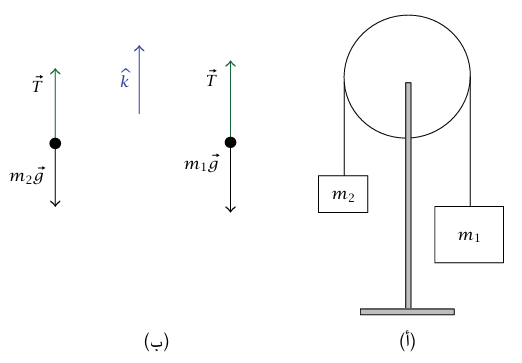
شكل 3–5: رسم توضيحي (أ) ومخطط الجسم الحر (ب) للمثال 3–4.

(إذا كان الوتر عديم الوزن والتلامس بين الوتر والبكرة أملس، فإن الشد عند الاتزان يكون هو نفسه عند جميع نقاط الوتر. كان الإثبات مبنيا على حقيقة أن القوة الكلية المؤثرة على كل عنصر صغير من الوتر تساوي صفرًا. حتى في حالة عدم الاتزان يجب أن تكون القوة المؤثرة على عنصر من وتر عديم الوزن تساوي صفرًا؛ إذا كان العنصر بلا وزن، فإنه يكون عديم الكتلة، ويقضي قانون نيوتن الثاني بأن القوة الكلية المؤثرة على عنصر ما تساوي كتلة العنصر (صفرا) مضروبة في عجلته. وهكذا نستطيع أن نبين كما سبق أن الشد هو نفسه عند جميع نقاط الوتر. حتى إذا كان التلامس بين الوتر والبكرة خشنًا، فإن الشد سيكون هو نفسه عند جميع نقاط الوتر إذا كانت البكرة عديمة الكتلة وتدور على محور أملس. إذا لم نذكر غير ذلك، فسوف يفترض أن الأوتار والبكرات عديمة الوزن والمحاور ملساء (لا احتكاكية).)

مثال 3–5 (تحليل آلة أتوود). لتحاشي لَبْس الإشارات، نُدخل متجه وحدة 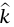 يشير رأسيًا إلى أعلى نعرف عجلة m₂ بأنها  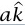(أي إنه إذا كانت a موجبة، فإن عجلة m₂ تتجه إلى أعلى). وحيث إن الوتر غير قابل للمطّ فرضًا، فإن عجلة m₁ هي 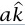–. اذا كان الشد في الوتر هو T، فإن معادلة القوة (قانون نيوتن الثاني) للكتلة m₂ هي:

يشيع خطأ أن تضع قائمة غير صحيحة للقوى المؤثرة على m₁ وm₂ في المثال السابق. القوتان المؤثرتان على m₁ هما شدُّ الجاذبية إلى أسفل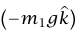، وشد الوتر إلى أعلى 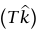. قوة الجاذبية التثاقلية على m₂ ليست قوةً مؤثرة على m₁، وT لا ينبغي أن تُستبدل بها القوة m₂g في معادلة القوة الخاصة بالكتلة m₁. بالمثل، T يجب ألا تستبدل بها القوة m₁g في معادلة القوة الخاصة بالكتلة m₂.

يجب أن يكتسب المرء عادةَ فَحْص الإجابة ليرى ما إذا كانت «معقولة». وعلى وجه الخصوص، توجد عادةً حالات خاصة محددة نعرف فيها بالفعل ما هي الإجابة، وإذا كانت إجابتنا صحيحة، فإنها سوف تؤول إلى القيمة المتوقعة في هذه الحالات الخاصة. هذا الإجراء سوف يمكننا عادةً من اكتشاف الأخطاء الجبرية، بالإضافة إلى الأخطاء في الاستنتاج.

نتوقع في المثال السابق أن يكون 0 = a إذا كان m₁ = m₂، و0 < a إذا كان m₁ > m₂. و0 > a إذا كان m₁ < m₂. المعادلة (8–3) تتفق مع هذه التوقعات. فضلا عن ذلك، إذا كان m₁ = m₂ يكون لدينا اتزان، ومن ثَمَّ نتوقع أن يكون T = m₁g والمعادلة (9–3) تتفق مع هذا التوقع إذا اعتبرنا m₁ = m₂. ونعلم الإجابة أيضًا، بدون حساب، في الحالة الخاصة عندما تكون m₁ أكبر كثيرًا من m₂. في هذه الحالة نتوقع أن تسقط m₁ مثل الجسم الذي يسقط بحرِّيَّة؛ أي إن a = g في حقيقة الأمر، المعادلة (8–3) تؤدي إلى هذه النتيجة عندما يكون m₁ ≫ m₂ (يمكننا إهمال m₂ في البسط والمقام)، وتعطي أيضًا و g– = a (كما هو متوقع) عندما يكون
m₂ ≫ m₁. زيادة على ذلك؛ حيث إن m₂ تتسارع إلى أعلى بعجلة g عندما يكون m₁ ≫ m₂، فإنه ينتج في هذه الحالة أن القوة الكلية المؤثرة على m₂ يجب أن يكون مقدارها 2m₂g، ويجب أن يكون اتجاهها إلى أعلى؛ لهذا يجب أن يكون الشد في الوتر 2m₂g عندما يكون m₁ ≫ m₂. المعادلة (9–3) تثبت هذا وتؤكِّده لأن m₁ / (m₁ + m₂) تقترب من الواحد عندما يكون m₁ ≫m₂.

مثال 3–6 (تآثر آلة أتوود مع الأرضية). هناك سؤال يتردد كثيرًا حول مثال 3–5 وهو التالي: ما القوة المتجهة إلى أعلى 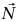 التي تؤثر بها الأرض على الحامل؟ (بمعنى آخر، إذا وضع الجهاز بأكمله على المقياس، فما هي القراءة التي سوف يبينها المقياس؟) إذا كان الجهاز بأكمله في حالة اتزان يمكننا على الفور أن نستدلَّ من قانون نيوتن الأول على أن  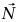تساوي في المقدار وزن الجهاز. لكن m₁ وm₂ تتحركان بعجلة، ومن ثُمَّ فهما ليستا في حالة اتزان.

من المفيد عند هذه النقطة أن يمتد قانون نيوتن الثاني ليُطبق على الأنظمة المركبة (المكونة من أكثر من جسيم واحد)، تمامًا مثلما فعلنا مع قانون نيوتن الأول. ببساطة نكتب المعادلة  لكل جسيم في نظامنا قيد الاعتبار (الدليل i يعدد الجسيمات)، ونجمع المعادلات الناتجة لنحصل على . إذا حللنا  إلى جزء خارجي وجزء داخلي، فإن القوى الداخلية تتلاشى زوجًا زوجًا نتيجةً لقانون نيوتن الثالث؛ وبهذا نحصل على:

حيث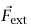 هي القوة الخارجية الكلية (أي صافي القوة أو الحاصل المتجهي) المؤثرة على النظام.

إذا كانت كل جسيمات النظام لها نفس العجلة ، فإن المعادلة (10–3) تصبح:

حيث M الكتلة الكلية للنظام.

دَعْنَا نطبق المعادلة (10–3) على آلة أتوود، معتبرين أن النظام هو الجهاز بأكمله (يشمل الحامل الذي يُفترض أنه عديم الوزن). لا نستطيع استخدام المعادلة (11–3) لأن أجزاء النظام المختلفة لها تسارعات مختلفة؛ ولهذا يجب أن نستخدم المعادلة (10–3). القوتان الخارجيتان الوحيدتان المؤثرتان على هذا النظام هما الجاذبية الأرضية والقوة العمودية التي تؤثر بها الأرض. بهذا تنص المعادلة (10–3) على أن:

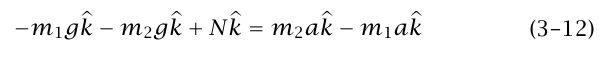
وتعطي N = (m₂ – m₁) a + (m₁ + m₂) g بإدخال معادلتنا السابقة (8–3) للتعويض عن a وإجراء قليل من الجبر، نحصل على:

إذا لم يكن الحامل بلا وزن، فإنه يجب أن تتضمن القوةُ الخارجية وزن الحامل، ويضاف ببساطة إلى الطرف الأيمن للمعادلة (13–3). لاحظ أنه عندما يكون m₁ = m₂ نجد من المعادلة (13–3) أن N = 2m₁g، وهو ما نتوقعه في حالة الاتزان. إذا كان m₁ ≠ m₂، فإنه ينتج من المعادلة (13–3) أن N < m₁g + m₂g. وبناءً على ذلك، إذا وضع الجهاز على مقياس، فإن المقياس سوف يقرأ أقل من وزن الجهاز!

على الرغم من أننا حسبنا N باستخدام معادلة النظرية العامة (10–3)، فإنه يمكننا أيضًا إيجاد N بملاحظة أن الحامل في حالة اتزان القوى الخارجية الوحيدة التي تؤثر على الحامل هي قوتا الشد في الوترين إلى أسفل، كلٌّ منهما بقوة T، ودفع الأرضية إلى أعلى بقوة مقدارها N. وبهذا نجد أن N = 2T، وباستخدام المعادلة (9–3) للتعويض عن T نحصل على المعادلة (13–3).

مثال 3–7 (تحليل نظام بكرات مزدوج). دعنا نعتبر نظام البكرات المبين في شكل 3–6 (أ). البكرتان ملساوان ولا وزن لهما موضع البكرة B ثابت، بينما A يمكنها أن تتحرك. لقد رأينا بالفعل (مثال (72) أنه إذا كان m₁ = (1/2) m₂ فإن النظام سيكون في حالة اتزان إذا اختيرت m₁ وm₂ عشوائيا، فإننا نريد حساب عجلتي كلٌّ من الكتلتين والشد T في الوتر.

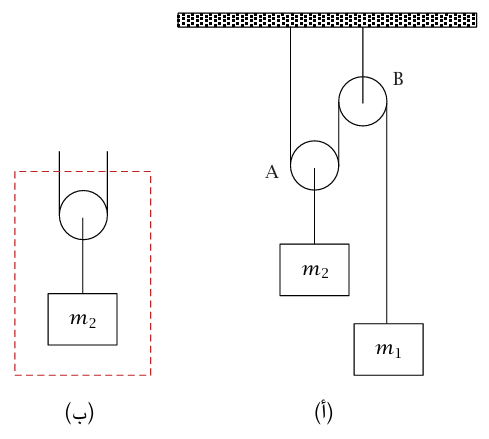
شكل 3–6: (أ) رسم توضيحي لمثال 3–7. (ب) من المفيد اعتبار النظام الفرعي في الصندوق المتقطع.

من الضروري التعرُّف على العلاقة بين عجلة m₂ وعجلة m₁. العجز عن فهم هذه العلاقة، التي هي نتيجة مباشرة لحقيقة أن الطول الكلي للوتر يظل ثابتًا، يعتبر خطأ مصدر شائع جدا. ولكي يظل الوتر مربوطًا، فإن m₁ يجب أن تهبط بوصتين مقابل كل بوصة ترتفعها m₂. إذا أدخلنا متجه وحدة 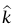 يشير رأسيًّا إلى أعلى، وعرَّفنا عجلة m₂ بأنها 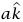، فإن عجلة m₁ حينئذ تكون –.

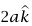بتطبيق قانون نيوتن الثاني على m₁ نجد أن 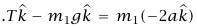 وبتطبيق قانون نيوتن الثاني على m₂ (أو بدقة أكثر، على النظام الذي يحتويه الصندوق المنقطع في شكل 3–6 (ب )) نجد أن

بحل هاتين المعادلتين الآتيتين لإيجاد a وT نحصل على:

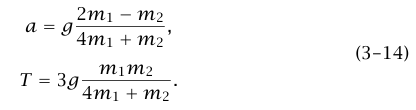
عندما يكون = (1/2) m₂  m₁ فإننا نستعيد مسألة الاستاتيكا. على القارئ أن يتحقق من أن معادلتي a وT تئولان إلى القيمتين المتوقعتين عندما يكون m₁ ≫m₂، وعندما يكون m₂ ≫m₁.

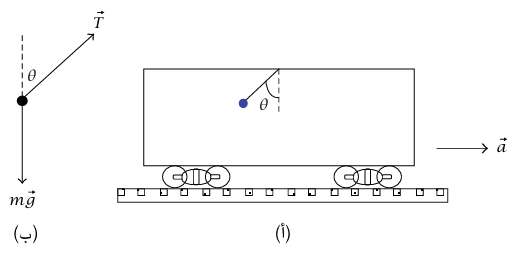
شكل 3–7: رسم توضيحي (أ). ومخطط الجسم الحر (ب) للمثال 3–8.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل