مايكل كوهين

الميكانيكا الكلاسيكية مقدمة أساسية

ص 87 – ص 89

طبقًا لقانون نيوتن الأول، تظل السرعة ثابتة عندما لا تؤثر على الجسم قوة محصلة. ويخبرنا قانون نيوتن الثاني بطريقة كمية عن كيفية تعديل الجسم لسرعته عندما تؤثّر عليه قوة ما.

بكلمات نيوتن نفسه: «يتناسب تغير الحركة طرديا مع القوة المحركة، ويكون في اتجاه الخط المستقيم الذي تؤثّر فيه تلك القوة.» ¹ ليست جميع الكلمات الواردة في هذا النص مألوفة للفيزيائي المعاصر. يعرف نيوتن «الحركة» بأنها حاصل ضرب «كمية المادة» في السرعة، و«الحركة» عند نيوتن الآن تُسمَّى «كمية التحرك»، كما أن «تغير الحركة» يعني لديه «معدل التغير في الحركة».

ويعبر عن هذا بلغة المتجهات الدقيقة على الصورة

رمزان من الرموز الثلاثة في المعادلة (1–3) تم تعريفهما فعلًا: 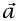 كمية كينماتيكية صرفة وهي تمثل متجه العجلة، و تمثل متجه القوة. أما الرمز الثالث (m) فيتطلب بعض المناقشة؛ ذلك أن تعريف «الكتلة» بأنها «كمية المادة» غير واضح إلى حدٍّ ما تتيح لنا المعادلة (1–3) أن نستنبط إجراء عمليا دقيقًا لقياس كتلة ما تنص المعادلة على أنه إذا أخضعنا جسمًا معيَّنا لقوى مختلفة، فإن عجلة الجسم تتناسب مع القوة المؤثرة عليه؛ أي إن  وثابت التناسب k خاصية للجسم؛ فكلما كانت قيمة k أكبر، كان تعجيل الجسم أيسر. وتُعرَّف كتلة الجسم بأنها مقلوب k؛ أي إن m = 1/k.

الكميات الأساسية في النظام الإنجليزي للوحدات هي: الطول (قدم)، والزمن (ثوان)، والقوة (أرطال). وقد عُرف الرطل بأنه القوة التي تؤثّر بها الأرض على جسم عياري معين موضوع في مكان معين يمكننا استخدام المعادلة (1–3) لتعيين الكتلة m لجسم ما. الكتلة هي القوة المؤثرة على الجسم (مقيسة بالأرطال) مقسومة على العجلة (مقيسة بوحدات ft/sec²). الوحدة الإنجليزية للكتلة تُسمَّى «سلج»، وهي وحدة مشتقة أبعادها lb–sec²/ft الجسم الذي كتلته 1 سلج يكتسب عجلة مقدارها  ft/sec²1 عندما يتعرض لقوة مقدارها 1 رطل والجسم الذي كتلته 2 سلج سوف يكتسب عجلة مقدارها 0.5 ft/sec2  عندما يتعرض لقوة مقدارها 1 رطل، وهكذا.

دَعْنَا نطبق المعادلة (1–3) على جسم وزنه W يسقط بحرية عند «موضع عياري». وجد عمليًّا أن جميع الأجسام التي تسقط بحرية يكون لها نفس العجلة عند مكان معين؛ وعند الموضع العياري تكون القيمة العددية لهذه العجلة (المسماة g) هي ft/sec² 32.174، والمعادلة (1–3) تقول إن mg = W. بهذا تكون الكتلة m لجسم ما مرتبطة بوزنه W بالمعادلة

لاحظ أن W وg تعتمدان على المكان الذي يوجد فيه الجسم، لكن قانون نيوتن الثاني يؤكد أن m خاصية للجسم لا تعتمد على موضعه. فالجسم الذي كتلته 1 سلج يزن 32.147 رطلًا عند الموضع العياري، لكنَّ وزنه يمكن أن يختلف قليلا عند مكان آخر.

النظام المتري، الوحدات الأساسية هي: الطول (أمتار)، والزمن (ثوان)، والكتلة (كيلوجرامات). الكيلوجرام يمكن تعريفه بأنه كتلة 1000 سنتيمتر مكعب من الماء تحت الظروف العيارية لدرجة الحرارة والضغط، لكن لمزيد من الدقة يمكن تعريفه أخيرًا بدلالة ثوابت أساسية أخرى الوحدة المترية للقوة، النيوتن، هي القوة التي يجب تطبيقها على جسم ما كتلته كيلوجرام واحد لكي تكسبه عجلة مقدارها 1 متر / ثانية. النيوتن الواحد يساوي نحو 0.225 رطلًا، والرطل الواحد يساوي 4.45 نيوتن تقريبًا.

حالما يكون لدينا جسم كتلته الوحدة، فإننا نستطيع قياس كتلة جسم آخر بتعريضه مع الجسم العياري لنفس القوة، وقياس النسبة بين عجلتي الجسمين. إذا طبقت نفس القوة على الجسم رقم 1 والجسم رقم 2 يكون لدينا M₁a₁ = M₂a₂ وبالتالي إذا كانت 1 = ₁M يكون لدينا ₂a / ₁a = ₂M. لاحظ أن هذا الإجراء لقياس الكتل لا يتطلب وزن الجسم، ولا يتطلب حساب عدد البروتونات والنيوترونات والإلكترونات في الجسم. (يبدو من البديهي أنه إذا كان الجسم مؤلفًا من جسيمات (بروتونات ونيوترونات وإلكترونات) فإن كتلة الجسم تساوي مجموع كتل مكوناته. لكن، إذا كانت النيوترونات والبروتونات متجمعة لتكون نواة ثقيلة، فقد وجد أن كتلة النواة تكون أقل بحوالي 1% من مجموع كتل الجسيمات المكونة لها. توقع أينشتاين (على صواب) أن هذا «النقص في الكتلة» يساوي الشغل اللازم لتفكيك النواة مقسوما على مربع سرعة الضوء. وبهذا يصعب الدفاع عن فكرة نيوتن عن الكتلة باعتبارها «كمية المادة» عندما تكون الجسيمات مرتبطة معًا بقوة نووية شديدة جدًّا. بالمثل، وزن النواة يكون أقل بقدر ملموس من مجموع أوزان الجسيمات المكونة لها. وبرغم هذا فإن جميع الأجسام (بروتونات، نيوترونات أنوية، كرات بيسبول) تسقط بنفس العجلة g عند أي مكان بعينه. هذه الحقيقة تُحقق منها بدقة عالية لدرجة لا يمكن تخيلها. ² وهكذا فإن تناسبية الوزن والكتلة التي تعبر عنها المعادلة W = mg، تبدو أنها قانون طبيعي فوق النقد بكثير عن مجرد عملية جمع للوزن أو الكتلة. في الحياة اليومية، حيث لا تؤخذ القوى النووية في الحسبان، يكون «نقص الكتلة» صغيرًا جدًّا، وتظل خاصية الجمع صحيحة لجميع الأغراض العملية.)

إذا كان 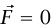 فإن المعادلة (1–3) تقول إن 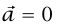؛ ولهذا تكون السرعة  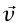ثابتة. وهكذا يتضح أن القانون الثاني يتضمن القانون الأول كحالة خاصة.

___________________________________________
هوامش

(1) Isaac Newton, Principia Mathematica, edited, with commentary by Stephen Hawking, Google Books reference, available at http://books.google.com/books.

 (2) Gerald Holton and Stephen G. Brush, From Copernicus to einstein and beyond, Addison-Wesley, Rutgers University Press, Piscataway, NJ, 2001.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل