الحركة التي تكون العجلة فيها ثابتة مع الزمن تُعد حالة خاصة مهمة. سوف نجد بعد قليل أن هذه الحالة تحدث كلما كانت القوى هي نفسها دائمًا عند أي زمن. إن المنحنى البياني للعجلة مقابل الزمن بسيط (شكل 1–7). المساحة تحت جزء هذا المنحنى البياني الواقع بين الزمن صفر وزمن t تساوي a . t. وبذلك يكون t) – v(0) = at)v. لكي نصل إلى التعبير المستخدم بصورة شائعة نكتب v بدلًا من (t) v و v₀ بدلا من (0) v. بذلك يكون:

الرسم البياني v مقابل t (شكل 1–8) عبارة عن خط مستقيم ميله a. يمكننا الحصول على علاقة صريحة لـ (t)x عن طريق إدخال هذه العلاقة في المعادلة (3–1) وإجراء التكامل أو – بدون حساب التكامل – عن طريق حساب المساحة المظللة تحت الخط في شكل 1–8 بين 0 = t و t. هندسيًّا (شكل 1–9)، تكون المساحة تحت شكل 1–8 بين 0 = t وt هي العرض t مضروبا في الارتفاع عند نقطة المنتصف وهو
1/2 (v_o + v_o + at). وبذلك نجد أن x(t) – xo = 1/2 (2v_ot + at²). وأخيرًا يكون:

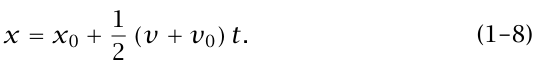
إذا أردنا استخدام حساب التفاضل والتكامل (أي: معادلة (3–1))، نكتب:

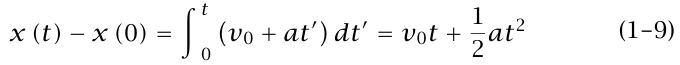
(لاحظ أننا أعدنا تسمية متغير التكامل «الوهمي» t' لتجنب الخلط بينه وبين النهاية العظمى t للتكامل.)

بمقارنة المعادلة (8–1) مع تعريف السرعة المتوسطة (معادلة (1–1)) نجد أن السرعة المتوسطة خلال أي فترة زمنية تساوي نصف مجموع السرعتين الابتدائية والنهائية. وفيما عدا حالات خاصة، يكون هذا صحيحًا فقط للحركة ذات العجلة المنتظمة.

نرغب أحيانًا في معرفة السرعة كدالة للموضع x بدلا من أن تكون دالة للزمن t. بحل المعادلة (7–1) لـ t، أي a/ (v–v₀) = t والتعويض في المعادلة (8–1) نحصل على:

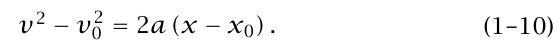
نقوم هنا بتجميع العلاقات الرياضياتية التي سبق اشتقاقها، والقابلة جميعها للتطبيق فقط في حالة الحركة بعجلة ثابتة.

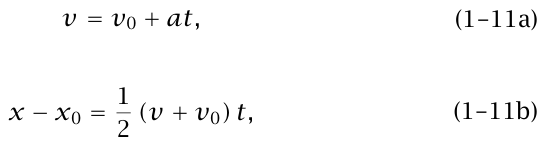
شكل (1–8) رسم السرعة مقابل الزمن لعجلة ثابتة.

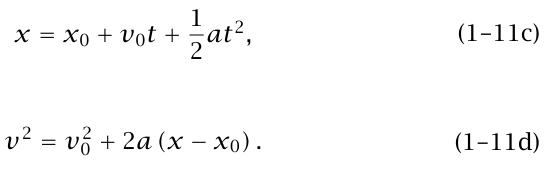
هناك غالبًا أكثر من طريقة لحل مسألة ما، ولكن كل الطرق ليست بنفس الكفاءة. فعلى حسب المعلومات المعطاة والسؤال المطروح، تؤدي عادة إحدى العلاقات السابقة أعلاه إلى الجواب مباشرة.

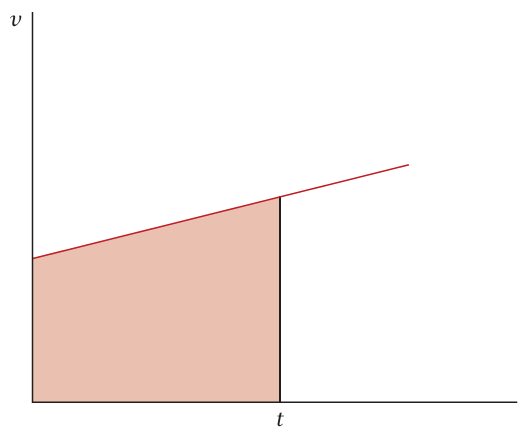
شكل 1–9: المساحة تحت المنحنى v مقابل t.

مثال 1–4 (مسألة عجلة ثابتة). تتباطأ سيارة (بعجلة تناقصية ثابتة) م mph  60 إلى السكون خلال مسافة ft 500. [لاحظ أن 60 mph = 88 ft/sec]

(1) احسب العجلة.

(2) كم استغرقت من الوقت؟

(3) ما المسافة التي قطعتها السيارة منذ لحظة بداية عمل المكابح إلى اللحظة التي كان عندها مقدار السرعة 30 mph؟

(4) إذا كانت السيارة تسير بسرعة مقدارها 90 mph عند بدء عمل المكابح، بينما كان التباطؤ كما هو سابقًا، كيف سيتغير كل من مسافة التوقف وزمن التوقف؟

مثال 1–5 (مثال آخر للعجلة الثابتة). تتسارع سيارة سباق بعجلة ثابتة على شريط اندفاع مستقيم. تمر السيارة برادار (رقم 1) يقيس سرعتها اللحظية بمقدار 60 ft/s بعدها تمر برادار ثان (رقم 2) يقيس سرعتها اللحظية بمقدار ft/s 150.

(1) ما مقدار سرعتها عند منتصف الفترة الزمنية) بين القياسين؟

(2) ما مقدار سرعتها عندما تكون في منتصف المسافة بين الرادارين؟

(3) إذا كانت المسافة بين الرادارين هي ft  500 كم تبعد نقطة البداية عن الرادار (رقم 1)؟

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل