Tangential Distance, Velocity and Acceleration

So far we have used the model of a rotating shaft to illustrate the concepts of angular distance, velocity and acceleration. We now wish to shift the focus of our discussion to the dynamics of a particle traveling along a circular path. For this we will use the model of a small mass m on the end of a massless stick of length r shown in Figure (1). The other end of the stick is attached to and is free to rotate about a fixed axis at the origin of our coordinate system. The presence of the stick ensures that the mass m travels only along a circular path of radius r. The quantity θ( t ) is the angular distance travelled and ω( t ) the angular velocity of the particle.
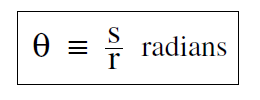.......(i)

When we are discussing the motion of a particle in a circular orbit, we often want to know how far the particle has travelled, or how fast it is moving. The distance s along the path (we could call the tangential distance) travelled is given by Equation (i) as

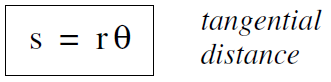........(1)

Figure 1: Mass rotating on the end of a massless stick.

The speed of the particle along the path, which we can call the tangential speed v_t, is the time derivative of the tangential distance s(t)

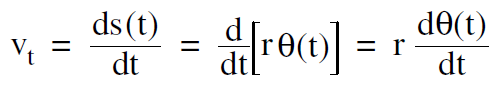
where r comes outside the derivative since it is constant. Since dθ (t) /dt is the angular velocity ω, we get

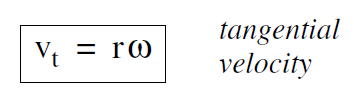
The tangential acceleration a_t , the acceleration of the particle along its path, is the time derivative of the tangential velocity

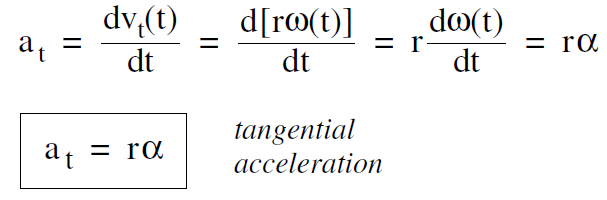
where again we took the constant r outside the derivative, and used α = dω/dt .

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل