RADIAN MEASURE

From the point of view of doing calculations, it is more convenient to measure an angle in radians than the more familiar degrees. In radian measure the angle θ shown in Figure (1) is the ratio of the arc length s to the radius r of the circle
.........(1)
Since s and r are both distances, the ratio s/r is a dimensionless quantity. However we will find it convenient for the angular analogy to keep the name radians as if it were the actual dimension of the angle. For example we will measure angular velocities in radians per second, which is analogous to linear velocities measured in meters per second.
Since the circumference of a circle is 2π r , the number of radians in a complete circle is

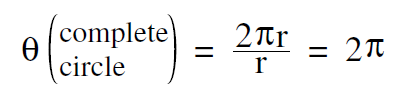
In discussing rotation, we will often refer to going around one complete time as one complete cycle. In one cycle, the angle θ increases by 2π . Thus 2π is the number of radians per cycle. We will find it convenient to assign these dimensions to the number 2π :

..........(2)

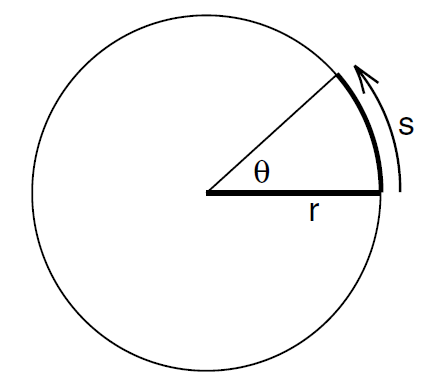
Figure 1: The angle θ in radians is defined as the ratio of the arc length s to the radius r: θ = s /r .

To relate radians to degrees, we use the fact that there are 360 degrees/cycle and dimensional analysis to find the number of degrees/radian

...........(3)

Fifty seven degrees is a fairly awkward unit angle for purposes of drafting and navigation; no one in his or her right mind would mark a compass in radians. However, in working with the dynamics of rotational motion, radian measure is the only reasonable choice.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل