Inclined Plane with Friction

In our analysis of the air cart on the inclined track, we mentioned that a frictionless surface exerts only a normal force on an object. If there is any sideways force, that is supposed to be a friction force 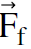. In Figure (1) we show a cart on an inclined plane, with a friction force  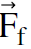included. The normal force 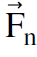is perpendicular to the plane, the friction force 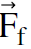is parallel to the plane, and gravity still points down.

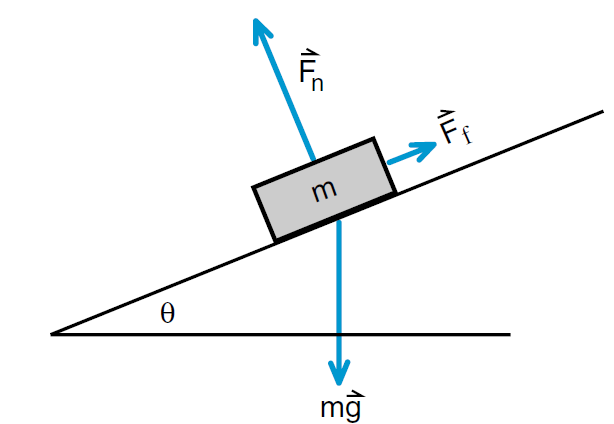
Figure 1: Friction force acting on the cart.

To analyze the motion of the cart when acted on by a friction force, we write Newton’s second law in the usual form

..........(1)

The only change is that we have added in the new force .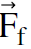
Since the motion of the cart is still along the plane, it is convenient to take the x axis along the plane as shown in Figure (2). Breaking Equation 1 up into x and y components now gives

...........(2a)

.........(2b)

From 2b we get,
F_n = mg cos θ...........(3)

which is the same result as for the frictionless plane.
The new result comes when we look at motion down the plane. Solving 2a for ax gives

a_x = gsinθ – F_f /m.......... (4)
Not surprisingly, the friction force reduces the acceleration down the plane.

Figure 2

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل