


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | Homotopies and the Fundamental Group-The Fundamental Group of a Topological Space |
|
|
|
Read More
Date: 31-5-2021
Date: 24-6-2017
Date: 26-5-2021
|
Definition Let X be a topological space, and let x0 and x1 be points of X.
A path in X from x0 to x1 is defined to be a continuous map γ: [0, 1] → X for which γ(0) = x0 and γ(1) = x1. A loop in X based at x0 is defined to be a continuous map γ: [0, 1] → X for which γ(0) = γ(1) = x0.
We can concatenate paths. Let γ1: [0, 1] → X and γ2: [0, 1] → X be paths in some topological space X. Suppose that γ1(1) = γ2(0). We define theproduct path γ1.γ2: [0, 1] → X by
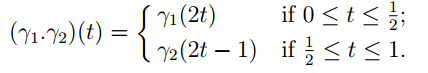
(The continuity of γ1.γ2 may be deduced from Lemma 1.1.)
If γ: [0, 1] → X is a path in X then we define the inverse path γ−1: [0, 1] →X by γ−1 (t) = γ(1−t). (Thus if γ is a path from the point x0 to the point x1 then γ−1 is the path from x1 to x0 obtained by traversing γ in the reverse direction.)
Let X be a topological space, and let x0 ∈ X be some chosen point of X.
We define an equivalence relation on the set of all (continuous) loops based at the basepoint x0 of X, where two such loops γ0 and γ1 are equivalent if and only if γ0 ≃ γ1 rel {0, 1}. We denote the equivalence class of a loop γ: [0, 1] → X based at x0 by [γ]. This equivalence class is referred to as the based homotopy class of the loop γ. The set of equivalence classes of loops based at x0 is denoted by π1(X, x0). Thus two loops γ0 and γ1 represent the same element of π1(X, x0) if and only if γ0≃ γ1 rel {0, 1} (i.e., there exists a homotopy F: [0, 1] × [0, 1] → X between γ0 and γ1 which maps (0, τ ) and (1, τ ) to x0 for all τ ∈ [0, 1]).
Theorem 1.2 Let X be a topological space, let x0 be some chosen point of X, and let π1(X, x0) be the set of all based homotopy classes of loops based at the point x0. Then π1(X, x0) is a group, the group multiplication on π1(X, x0) being defined according to the rule [γ1][γ2] = [γ1.γ2] for all loops γ1 and γ2 based at x0.
Proof First we show that the group operation on π1(X, x0) is well-defined.
Let γ1, γ΄1, γ2 and γ΄2 be loops in X based at the point x0. Suppose that [γ1] = [γ΄1] and [γ2] = [γ΄2]. Let the map F: [0, 1] × [0, 1] → X be defined by
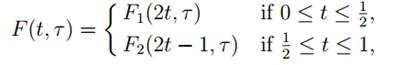
where F1: [0, 1] × [0, 1] → X is a homotopy between γ1 and γ΄1, F2: [0, 1] × [0, 1] → X is a homotopy between γ2 and γ΄2, and where the homotopiesF1 and F2 map (0, τ ) and (1, τ ) to x0 for all τ ∈ [0, 1]. Then F is itself a homotopy from γ1.γ2 to γ΄1.γ΄2, and maps (0, τ ) and (1, τ ) to x0 for all τ ∈ [0, 1]. Thus [γ1.γ2] = [γ΄1.γ΄2], showing that the group operation on π1(X, x0) is well-defined.
Next we show that the group operation on π1(X, x0) is associative. Let γ1, γ2 and γ3 be loops based at x0, and let α = (γ1.γ2).γ3. Then γ1.(γ2.γ3) = α◦θ, where
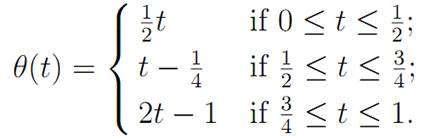
Thus the map G: [0, 1]×[0, 1] → X defined by G(t, τ ) = α((1−τ )t+τθ(t)) is a homotopy between (γ1.γ2).γ3 and γ1.(γ2.γ3), and moreover this homotopy maps (0, τ ) and (1, τ ) to x0 for all τ ∈ [0, 1]. It follows that (γ1.γ2).γ3 ≃γ1.(γ2.γ3) rel {0, 1} and hence ([γ1][γ2])[γ3] = [γ1]([γ2][γ3]). This shows that the group operation on π1(X, x0) is associative.
Let ε: [0, 1] → X denote the constant loop at x0, defined by ε(t) = x0 for all t ∈ [0, 1]. Then ε.γ = γ ◦ θ0 and γ.ε = γ ◦ θ1 for any loop γ based at x0, where
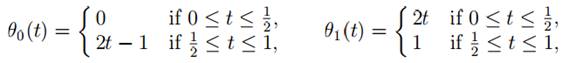
r all t ∈ [0, 1]. But the continuous map (t, τ ) → γ((1 − τ )t + τθj (t)) is a homotopy between γ and γ ◦ θj for j = 0, 1 which sends (0, τ ) and (1, τ ) to x0 for all τ ∈ [0, 1]. Therefore ε.γ ≃ γ ≃γ.ε rel {0, 1}, and hence [ε][γ] = [γ] = [γ][ε]. We conclude that [ε] represents the identity element of π1(X, x0).
It only remains to verify the existence of inverses. Now the map K: [0, 1]× [0, 1] → X defined by
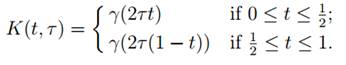
is a homotopy between the loops γ.γ−1 and ε, and moreover this homotopy
sends (0, τ ) and (1, τ ) to x0 for all τ ∈ [0, 1]. Therefore γ.γ−1 ≃ ε rel{0, 1}, and thus [γ][γ−1] = [γ.γ−1] = [ε]. On replacing γ by γ−1, we see also that [γ−1][γ] = [ε], and thus [γ−1] = [γ]−1, as required.
Let x0 be a point of some topological space X. The group π1(X, x0) is referred to as the fundamental group of X based at the point x0.
Let f: X → Y be a continuous map between topological spaces X and Y , and let x0 be a point of X. Then f induces a homomorphism f#: π1(X, x0) →π1(Y, f(x0)), where f#([γ]) = [f ◦ γ] for all loops γ: [0, 1] → X based at x0.
If x0, y0 and z0 are points belonging to topological spaces X, Y and Z, and if f: X → Y and g: Y → Z are continuous maps satisfying f(x0) = y0 and g(y0) = z0, then the induced homomorphisms f#: π1(X, x0) → π1(Y, y0) and g#: π1(Y, x0) → π1(Z, z0) satisfy g# ◦ f# = (g ◦ f)#. It follows easily from this that any homeomorphism of topological spaces induces a corresponding isomorphism of fundamental groups, and thus the fundamental group is a topological invariant.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|