المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Angles-Angles Around a Point |
 886
 02:19 مساءً
date: 12-3-2017 |
Author : المرجع الالكتروني للمعلوماتيه 
Book or Source : www.almerja.com 
Page and Part : ...|
Read More
Date: 12-3-2017
1083
Date: 14-3-2017
1862
Date: 12-3-2017
2199
|
Angles around a point will always add up to 360 degrees.
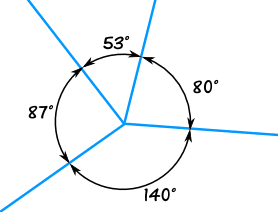
The angles above all add to 360°
53° + 80° + 140° + 87° = 360°
Because of this, we can find an unknown angle.
|
|
Example: What is angle "c"? To find angle c we take the sum of the known angles and take that from 360° Sum of known angles = 110° + 75° + 50° + 63° Angle c = 360° − 298° |
Angles On One Side of A Straight Line
Angles on one side of a straight line will always add to 180 degrees.
If a line is split into 2 and you know one angle you can always find the other one.
30° + 150° = 180°
Example: If we know one angle is 45° what is angle "a" ?
|
|
Angle a is 180° − 45° = 135° |
This method can be used for several angles on one side of a straight line.
Example: What is angle "b" ?
|
|
Angle b is 180° less the sum of the other angles. Sum of known angles = 45° + 39° + 24° Angle b = 180° − 108° |
Interior Angle
An Interior Angle is an angle inside a shape.
Exterior Angle
The Exterior Angle is the angle between any side of a shape, and a line extended from the next side.
Interior Angles of Polygons
An Interior Angle is an angle inside a shape.
Triangles
The Interior Angles of a Triangle add up to 180°
|
|
|
|
90° + 60° + 30° = 180° |
80° + 70° + 30° = 180° |
|
It works for this triangle! |
Let's tilt a line by 10° ... It still works, because one angle went up by 10°, but the other went down by 10° |
Quadrilaterals (Squares, etc)
(A Quadrilateral has 4 straight sides)
|
|
|
|
90° + 90° + 90° + 90° = 360° |
80° + 100° + 90° + 90° = 360° |
|
A Square adds up to 360° |
Let's tilt a line by 10° ... still adds up to 360°! |
|
The Interior Angles of a Quadrilateral add up to 360° |
|
Because there are Two Triangles in a Square
|
The interior angles in this triangle add up to 180° |
|
... and for this square they add up to 360° ... because the square can be made from two triangles! |
Pentagon
|
|
|
A pentagon has 5 sides, and can be made from three triangles, so you know what ... ... its interior angles add up to 3 × 180° = 540° And if it is a regular pentagon (all angles the same), then each angle is 540° / 5 = 108° (Exercise: make sure each triangle here adds up to 180°, and check that the pentagon's interior angles add up to 540°) |
|
|
The Interior Angles of a Pentagon add up to 540° |
|
The General Rule
Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total:
|
|
|
|
If it is a Regular Polygon (all sides are equal, all angles are equal) |
|
|
Shape |
Sides |
Sum of |
Shape |
Each Angle |
|
Triangle |
3 |
180° |
|
60° |
|
Quadrilateral |
4 |
360° |
|
90° |
|
Pentagon |
5 |
540° |
|
108° |
|
Hexagon |
6 |
720° |
|
120° |
|
Heptagon (or Septagon) |
7 |
900° |
|
128.57...° |
|
Octagon |
8 |
1080° |
|
135° |
|
Nonagon |
9 |
1260° |
|
140° |
|
... |
... |
.. |
... |
... |
|
Any Polygon |
n |
(n-2) × 180° |
|
(n-2) × 180° / n |
So the general rule is:
Sum of Interior Angles = (n-2) × 180°
Each Angle (of a Regular Polygon) = (n-2) × 180° / n
Perhaps an example will help:
Example: What about a Regular Decagon (10 sides) ?
|
|
And it is a Regular Decagon so: Each interior angle = 1440°/10 = 144° |
Exterior Angles of Polygons
The Exterior Angle is the angle between any side of a shape,
and a line extended from the next side.
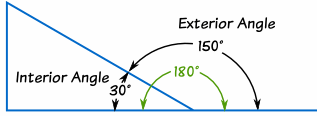
Note: when you add up the Interior Angle and Exterior Angle you get a straight line, 180°.
Polygons
A Polygon is any flat shape with straight sides
|
The Exterior Angles of a Polygon add up to 360° |
||
|
|
In other words the exterior angles add up to one full revolution (Exercise: try this with a square, then with some interesting polygon you invent yourself.)
|
|
|
Here is another way to think about it: |
|
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
