

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Angles
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
12-3-2017
3125

Names of Angles
As the Angle Increases, the Name Changes:
|
Type of Angle |
Description |
|
|
Acute Angle |
an angle that is less than 90° |
|
|
Right Angle |
an angle that is 90° exactly |
|
|
Obtuse Angle |
an angle that is greater than 90° but |
|
|
Straight Angle |
an angle that is 180° exactly |
|
|
Reflex Angle |
an angle that is greater than 180° |
|
In One Diagram This diagram might make it easier to remember: Also: Acute, Obtuse and Reflex are in alphabetical order. |
|
Be Careful What You Measure
|
|
|
|
This is an Obtuse Angle |
And this is a Reflex Angle |
|
|
|
|
But the lines are the same ... so when naming the angles make sure |
|
Positive and Negative Angles
When measuring from a line:
- a positive angle goes counterclockwise (opposite direction that clocks go)
- a negative angle goes clockwise

Example: −67°

Parts of an Angle
The corner point of an angle is called the vertex
And the two straight sides are called arms
The angle is the amount of turn between each arm.

Labelling Angles
|
There are two main ways to label angles: 1. give the angle a name, usually a lower-case letter like a or b, or sometimes a Greek letter like α (alpha) or θ (theta) 2. or by the three letters on the shape that define the angle, with the middle letter being where the angle actually is (its vertex). Example angle "a" is "BAC", and angle "θ" is "BCD"
Acute |
|
An Acute Angle is less than 90°

This is an acute angle
All the angles below are acute angles:

Which Angle?
Remember to look carefully at which angle you are being asked to name:
The acute angle is the small angle which is less than 90°.
|
If you choose the larger angle you would |
|
|
|
The smaller angle is an Acute Angle, |
Right Angles
A right angle is an internal angle which is equal to 90°

This is a right angle
Note the special symbol like a box in the angle. If you see this, it is a right angle. The 90° is rarely written in. If you see the box in the corner, you are being told it is a right angle.
All the angles below are right angles:
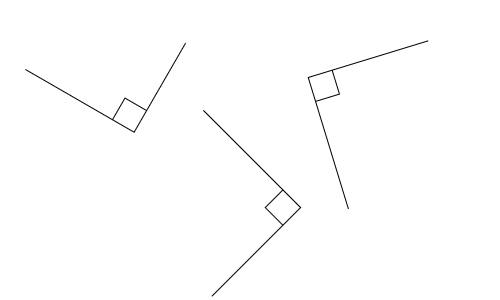
A right angle can be in any orientation or rotation as long as the internal angle is 90°
Obtuse Angle
An Obtuse Angle is more than 90° but less than 180°

This is an obtuse angle !
All the angles below are obtuse angles:

Straight Angle
A straight angle is 180 degrees

This is a straight angle
A straight angle changes the direction to point the opposite way.
Sometimes people say "You did a complete 180 on that!" ... meaning you completely changed your mind, idea or direction.
All the angles below are straight angles:

Reflex Angles
Different Angles have different names:
A Reflex Angle is more than 180° but less than 360°

This is a reflex angle
All the angles below are reflex angles:

Which Angle?
Remember to look carefully at which angle you are being asked to name.
The reflex angle is the larger angle.
It is more than 180° but less than 360°
If you choose the smaller angle you might have an Acute Angle, or an Obtuse Angle instead:
|
|
|
|
|
The larger angle is a Reflex Angle, |
|
The larger angle is a Reflex Angle, |
Full Rotation
A full rotation is 360 degrees

This is a "full rotation" or "revolution" or "complete turn" or "full circle"
Other ways of saying it:
- "I gave the wheel one complete turn looking for holes"
- "It was spinning at 200 revolutions per minute" (but people usually say "RPM" instead of "revolutions per minute").
- "Doing a 360" means you spin around completely once (spinning around twice is a "720").
- "It completed one cycle", meaning it went around exactly once.
- "She went full circle on liking carrots". So maybe she originally liked carrots, then hated them, now she likes them again.
|
This image of a protractor shows Also: Half a rotation is 180° Quarter of a rotation is 90° |
|
And a full rotation is also equal to 2π Radians, so here are some equivalent values:
|
Rotations |
Radians |
Degrees |
|
¼ |
π/2 |
90° |
|
½ |
π |
180° |
|
1 |
2π |
360° |
|
1½ |
3π |
540° |
|
2 |
4π |
720° |
 الاكثر قراءة في الهندسة المستوية
الاكثر قراءة في الهندسة المستوية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية























 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















