


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-3-2017
Date: 13-2-2019
Date: 17-2-2019
|
Point-slope refers to a method for graphing a linear equation on an x-y axis. When graphing a linear equation, the whole idea is to take pairs of x's and y's and plot them on the graph. While you could plot several points by just plugging in values of x, the point-slope form makes the whole process simpler. Point-slope form is also used to take a graph and find the equation of that particular line.
The point slope form gets its name because it uses a single point on the graph and the slope of the line. Think about it this way: You have a starting point on a map, and you are given a direction to head. You have all the information you need to draw a single line on the map.
The standard point-slope equation looks like this:
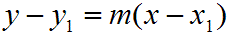
It should be noted that "y1" does not mean y multipled by 1. In this case it simply denotes a particular y value which you will plug into the equation. The variable m is the slope of the line.
Example 1
You are given the point (4,3) and a slope of 2. Find the equation for this line in point slope form.
Solution:
Just plug the given values into your point-slope formula above. Your point (4,3) is in the form of (x1,y1). That means where you see y1, use 3. Where you see x1, use 4. Your slope was given to you, so where you see m, use 2. Pretty simple, huh? Your final result should look like:
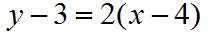
More Practice:
Your point is (-1,5). The slope is 1/2. Create the equation that describes this line in point-slope form. Try working it out on your own. The answer is: 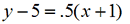 .
.
If that's not what you got, re-read the lesson and try again.
Point-slope form is all about having a single point and a direction (slope) and converting that between an algebraic equation and a graph. In the example above, we took a given set of point and slope and made an equation. Now let's take an equation and find out the point and slope so we can graph it.
Example 2
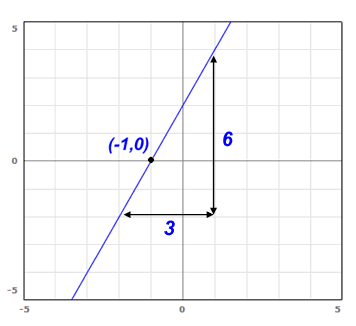
Find the equation (in point-slope form) for the line shown in this graph:
Solution:
To write the equation, we need two things: a point, and a slope. It is simple to find a point because we just need ANY point on the line. The point I've indicated, (-1,0), just happens to be the easiest one to find. Note also that it is useful to pick a point on the axis, because one of the values will be zero.
Finding the slope requires a little calculation, but it is also pretty easy. Just count the number of lines on the graph paper going in each direction of a triangle, like I've shown. Remember that slope is rise over run, or y/x. Therefore the slope of this line is 2. You could have used any triangle to figure out the slope and you would still get the same answer.
Putting it all together, our point is (-1,0) and our slope is 2. We know how to use the point-slope form, so the final answer is:
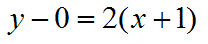



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|