Definition

A factor of a number is one that divides into the number evenly. That is, 6 is a factor of 12 because 12 divided by 6 is exactly 2. The number 5 is not a factor of 12, because 12 divided by 5 is 2.4.

It is easy to find all the factors of a small number, like 3. The only numbers that divide evenly into 3 are 1 and 3. Finding the factors of an enormous number, like 64,448, can be very hard, because there could be several hundred factors. You is more likely you will be asked to find factors of numbers somewhere in between those extremes, like 42, for example. The first step is to recognize that 42 is an even number, and is divisible by 2. That operation reveals another factor, 21.

Since 2 goes evenly into 42, the result must also be true. 21 goes into 42 twice. Now we have four factors: 42, 21, 2, and 1, since the number and 1 are always factors of any number. We know that there aren't any more numbers that divide into the 2, but 21 is 7 x 3. That means that 7 and 3 are also factors.

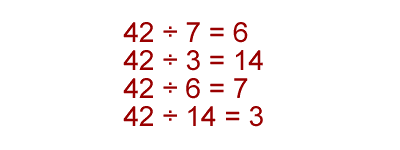
After dividing 42 by 7 and 3, we discovered the last two factors, 6 and 14. We now have a total of 8 factors: 42, 21, 14, 7, 6, 3, 2, 1. No combinations of those numbers will give us any more factors, so we must be finished factoring 42.

That number was easy enough to factor because it was even, so we could start with 2. What about a more difficult number, like 81? The best idea is to try a few small odd numbers, like 3,5 and 7, to see if any of them divide evenly. It is also a good idea to check the number to see if it is prime, in which case it would only have 2 factors: itself and 1.

Sure enough, 81 is divisible by 3, giving 27 as an answer. That means that atleast 1, 3, 27, and 81 are factors of 81. We know that 27 is 9 x 3, so 9 is an additional factor. No other numbers work, so 1, 3, 9, 27, and 81 are the only 5 factors of 81.