
Imaging the event horizon an outlook
 المؤلف:
Heino Falcke and Friedrich W Hehl
المؤلف:
Heino Falcke and Friedrich W Hehl
 المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
 الجزء والصفحة:
p 336
الجزء والصفحة:
p 336
 12-2-2017
12-2-2017
 2440
2440
Imaging the event horizon an outlook
One can easily see from the previous sections that the ever growing interest in Sgr A* has already yielded a number of tantalizing results, the most important being that Sgr A* is the best supermassive black hole candidate we know. VLBI observations are already approaching scales which are not far from the actual scale of the black hole and the presence of the sub-mm bump indicates that even more compact emission is present at yet smaller scales possibly as close in as the event horizon of the black hole. It is therefore worth exploring whether we have, in principle, a chance to actually approach this scale with imaging techniques
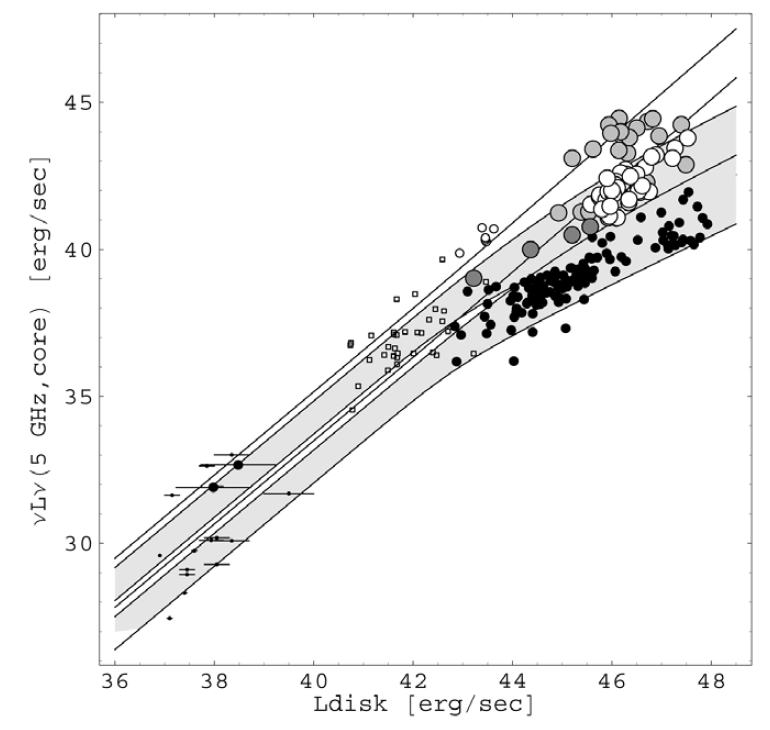
Figure 1.1. Correlation between thermal from the accretion disk (with the exception of X-ray binaries this is basically normalized to the narrow Hα emission) and the monochromatic luminosity of black hole radio cores: open circles, radio loud quasars; small open circles, FR I radio galaxies; open gray circles, blazars and radio intermediate quasars (dark grey); black dots, radio-quiet quasars and Seyferts; small dots, X-ray binaries; small boxes, detected sources from the ‘48 LINERs’ sample (Nagar et al 2000). The latter apparently confirm the basic prediction of Falcke and Biermann (1996) and almost close the gap between very low (on an absolute scale) accretion rate objects and high accretion rate objects. The shaded bands represent the radio-loud and radio quiet jet models as a function of accretion as shown in Falcke and Biermann (1996).
and to ask what we would expect to see. This naturally will have to be done at the highest radio frequencies where the resolution is the highest and the scatter broadening of Sgr A* is the lowest.
At sub-mm wavelengths, the various models indeed predict that the synchrotron emission of Sgr A* is not self-absorbed, allowing a view into the region near the event horizon. The size of this event horizon is 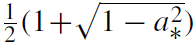 Rs, where RS ≡ 2GM/c2, M is the mass of the black hole, G is Newton's constant, c the speed of light, a∗ ≡ Jc/(GM2) is the dimensionless spin of the black hole in the range 0–1, and J is the angular momentum of the black hole.
Rs, where RS ≡ 2GM/c2, M is the mass of the black hole, G is Newton's constant, c the speed of light, a∗ ≡ Jc/(GM2) is the dimensionless spin of the black hole in the range 0–1, and J is the angular momentum of the black hole.
The appearance of the emitting region around a black hole was determined by Falcke et al (2000) from which we take the following discussion under the condition that it is optically thin. For Sgr A* this might be the case for the sub-mm bump (Falcke et al 1998) indicated by the turnover in the spectrum, and can always be achieved by going to a suitably high frequency. For the qualitative discussion the emissivity was assumed to be frequency independent and to be either spatially uniform or to scale as r−2. These two cases cover a large range of conditions expected under several reasonable scenarios, be it a quasi-spherical infall, a rotating thick disk, or the base of an outflow. The calculations took into account all the well-known relativistic effects, e.g. frame dragging, gravitational redshift, light bending, and Doppler boosting.
For a planar emitting source behind a black hole, a closed curve on the sky plane divides a region where geodesics intersect the horizon from a region whose geodesics miss the horizon (Bardeen 1973). This curve, which is referred to as the ‘apparent boundary’ of the black hole, is a circle of radius 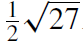 Rs in the Schwarzschild case (a∗ = 0), but has a more flattened shape of similar size for a Kerr black hole, slightly dependent on inclination. The size of the apparent boundary is much larger than the event horizon due to strong bending of light by the black hole. When the emission occurs in an optically thin region surrounding the black hole, the case of interest here, the apparent boundary has the same exact shape since the properties of the geodesics are independent of where the sources are located. However, photons on geodesics located within the apparent boundary that can still escape to the observer experience strong gravitational redshift and a shorter total path length, leading to a smaller integrated emissivity, while photons just outside the apparent boundary can orbit the black hole near the circular photon radius several times, adding to the observed intensity (Jaroszynski and Kurpiewski 1997). This produces a marked deficit of the observed intensity inside the apparent boundary the ‘shadow’ of the black hole.
Rs in the Schwarzschild case (a∗ = 0), but has a more flattened shape of similar size for a Kerr black hole, slightly dependent on inclination. The size of the apparent boundary is much larger than the event horizon due to strong bending of light by the black hole. When the emission occurs in an optically thin region surrounding the black hole, the case of interest here, the apparent boundary has the same exact shape since the properties of the geodesics are independent of where the sources are located. However, photons on geodesics located within the apparent boundary that can still escape to the observer experience strong gravitational redshift and a shorter total path length, leading to a smaller integrated emissivity, while photons just outside the apparent boundary can orbit the black hole near the circular photon radius several times, adding to the observed intensity (Jaroszynski and Kurpiewski 1997). This produces a marked deficit of the observed intensity inside the apparent boundary the ‘shadow’ of the black hole.
We here consider a compact, optically thin emitting region surrounding a black hole with spin parameter a∗ = 0 (i.e. a Schwarzschild black hole) and a maximally spinning Kerr hole with a∗ = 0.998. In the set of simulations shown in figure 1.2, the viewing angle i was taken to be 45o with respect to the spin axis (when it is present) with two distributions of the gas velocity v. The first has the plasma in free fall, i.e. vr = 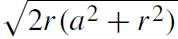 Δ/A and Ω = 2ar/A, where vr is the Boyer–Lindquist radial velocity, Ω is the orbital frequency, Δ ≡ r 2−2r +a2, and A ≡ (r 2 + a2)2 − a2 Δ sin2 θ. (We have set G = M = c = 1 in this paragraph.) The second has the plasma orbiting in rigidly rotating shells with the equatorial Keplerian frequency Ω = 1/(r 3/2 + a) for r > rms (marginally
Δ/A and Ω = 2ar/A, where vr is the Boyer–Lindquist radial velocity, Ω is the orbital frequency, Δ ≡ r 2−2r +a2, and A ≡ (r 2 + a2)2 − a2 Δ sin2 θ. (We have set G = M = c = 1 in this paragraph.) The second has the plasma orbiting in rigidly rotating shells with the equatorial Keplerian frequency Ω = 1/(r 3/2 + a) for r > rms (marginally
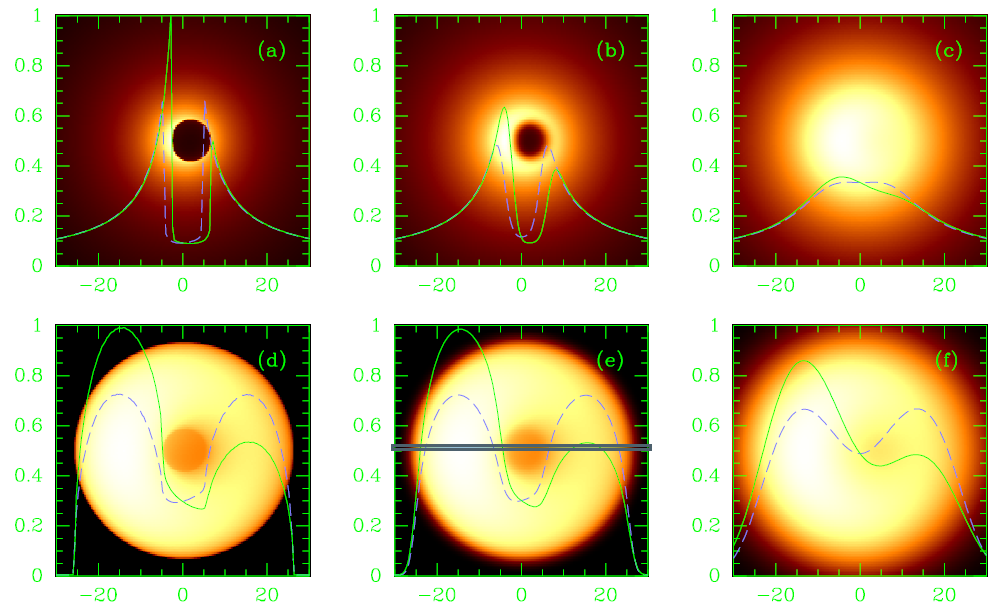
Figure 1.2. An image of an optically thin emission region surrounding a black hole with the characteristics of Sgr A* at the Galactic Center. The black hole is here either maximally rotating (a∗ = 0.998, panels (a)-(c)) or non-rotating (a∗ = 0, panels (d)–(f )). The emitting gas is assumed to be in free fall with an emissivity ∝ r−2 (top) or on Keplerian shells (bottom) with a uniform emissivity (viewing angle i = 45o). Panels (a) and (d) show the GR ray-tracing calculations, panels (b) and (e) are the images seen by an idealized VLBI array at 0.6 mm wavelength taking interstellar scattering into account, and panels (c) and (f ) are those for a wavelength of 1.3 mm. The intensity variations along the x-axis (full green curve) and the y-axis (dashed purple/blue curve) are overlaid. The vertical axes show the intensity of the curves in arbitrary units and the horizontal axes show the distance from the black hole in units of GM●/c2 (1/2RS). See also color section and video at.
stable radius) with v r = 0, and infalling with constant angular momentum inside r < rms (Cunningham 1975), with vθ = 0 for all r .
In order to display concrete examples of how realistic the proposed measurements of these effects with VLBI will be, the expected images were simulated for the massive black hole candidate Sgr A* at the Galactic Center.
The results of the two different models with and without scattering at two different observing wavelengths are shown in figure 1.2. The two distinct features that are evident in the top panel for a rotating black hole are: (1) the clear depression in Iν the shadow produced near the black hole, which in this particular example represents a modulation of up to 90% in intensity from peak to trough; and (2) the size of the shadow, which here is 4.6 RS in diameter. This represents a projected size of 34 μarcseconds. Such a resolution has already been surpassed in some λ2 mm-VLBI experiments of other radio cores (Krichbaum et al 2002). The shadow is a generic feature of various other models one can look at, including those with outflows, cylindrical emissivity, and various inclinations or spins.
This black hole shadow is also visible in the second illustrated case for a non-rotating black hole with a modulation in Iν in the range of 50-75% from peak to trough, and with a diameter of roughly 5.2 RS. In this case, the emission is asymmetric due to the strong Doppler shifts associated with the emission by a rapidly moving plasma along the line-of-sight (with velocity vφ).
The important conclusion is that the diameter of the shadow in marked contrast to the event horizon is fairly independent of the black hole spin and is always of order 5 RS. The presence of a rotating hole viewed edge-on will lead to a shifting of the apparent boundary (by as much as 1.25 RS, or 9 μarcseconds) with respect to the center of mass, or the centroid of the outer emission region. Another possible signature of general relativistic effects may come from the polarization properties of the sub-mm-wave emission region. This has been calculated by Bromley et al (2001).
The importance of the proposed imaging of Sgr A* at sub-mm wavelengths with VLBI cannot be overemphasized. The sub-mm bump in the spectrum of Sgr A* strongly suggests the presence of a compact component whose proximity to the event horizon is predicted to result in a shadow of measurable dimensions in the intensity map. Such a feature seems unique and Sgr A* seems to have all the right parameters to make it observable. The observation of this shadow would confirm the widely held belief that most of the dark mass concentration in the nuclei of galaxies such as ours is contained within a black hole, and it would be the first direct evidence for the existence of an event horizon largely independent of any modeling. It would finally turn the theoretical concept of an event horizon discussed at the beginning of the book into an observable reality.
A non-detection with sufficiently developed techniques, however, might pose a major problem for the standard black hole paradigm. Because of this fundamental importance, the experiment proposed here should be a major motivation for intensifying the current development of sub-mm astronomy in general and mm and sub-mm VLBI in particular.
This result also shows the outstanding position Sgr A* has among known radio cores and supermassive black hole candidates. For other supermassive black holes, with the exception perhaps of the very massive black hole in M87, the shadow will be much smaller than in Sgr A* because of the much larger distances.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


