
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Equations of motion of a free test particle
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 140
2-2-2017
1860
Equations of motion of a free test particle
1.1 Integrals of motion
Conserved quantities connected with Killing vectors ξ(t ) and ξ(φ) are:
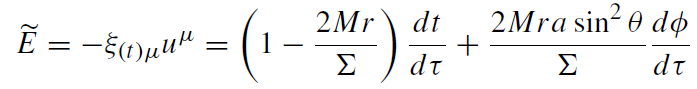 (1.1)
(1.1)
 (1.2)
(1.2)
As before, Ẽ = E/m is the specific energy and lz = Lz/m is the specific angular momentum of a particle. A conserved quantity connected with the Killing tensor is
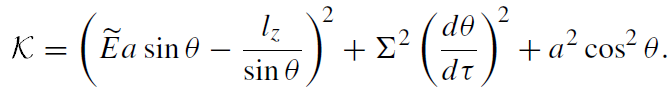 (1.3)
(1.3)
Quite often, one uses, instead of  , another integral of motion,
, another integral of motion, 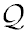 , that is related to it by
, that is related to it by
 (1.4)
(1.4)
To summarize, the equations of motion of a particle in the Kerr–Newman spacetime allow four integrals of motion, E, Lz , 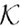 (or
(or 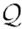 ), and a trivial one, uμuμ = −1.
), and a trivial one, uμuμ = −1.
1.2 First integrals of the equations of motion
One can express the four components uμ of the velocity as explicit functions of these integrals of motion and coordinates r and θ. As a result one gets the system
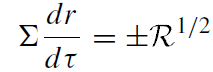 (1.5)
(1.5)
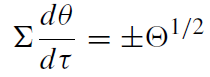 (1.6)
(1.6)
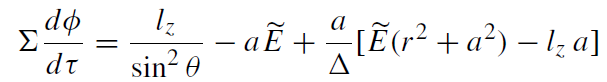 (1.7)
(1.7)
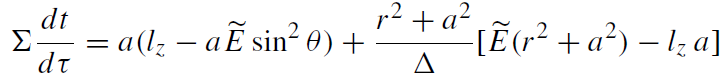 (1.8)
(1.8)
where
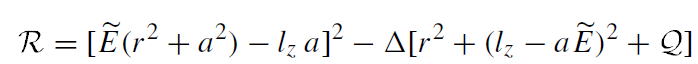 (1.9)
(1.9)
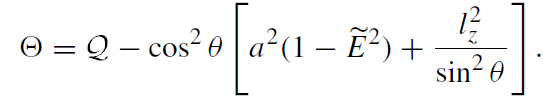 (1.10)
(1.10)
The signs ± which enter these relations are independent from one another. In the limit a → 0, that is for a non-rotating black hole, these equations coincide with the corresponding equations of motion in the tilted spherical coordinates. In this limit 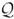 = l2 − l2z .
= l2 − l2z .
1.3 Bound and unbound motion
The geodesic world line of a particle in the Kerr metric is completely determined by the first integrals of motion Ẽ, lz, and 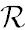 . Consider
. Consider  which enters the radial equation of motion as a function of r for fixed values of the other parameters:
which enters the radial equation of motion as a function of r for fixed values of the other parameters:
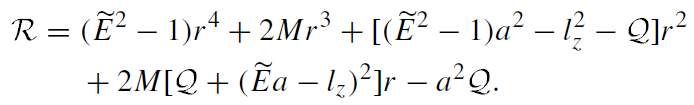 (1.11)
(1.11)
The leading term for large r on the right-hand side is positive if Ẽ2 > 1. Only in this case can the motion be infinite. For E2 < 1 the motion is always finite, i.e. the particle cannot reach infinity.
1.4 Effective potential
For a rotating black hole the variety of trajectories becomes wider and their classification is much more. We discuss only some important classes of trajectories.
For studying the qualitative characteristics of the motion of test particles in the Kerr metric it is convenient to use the effective potential. Let us rewrite  as
as
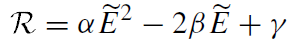 (1.12)
(1.12)
where
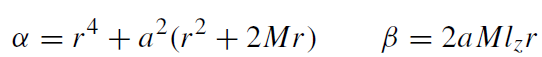 (1.13)
(1.13)
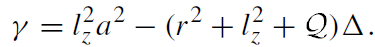 (1.14)
(1.14)
The radial turning points  = 0, see (1.1), are determined by the condition Ẽ = V±(r), where
= 0, see (1.1), are determined by the condition Ẽ = V±(r), where
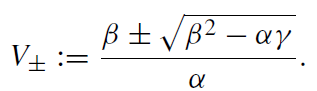 (1.15)
(1.15)
The quantities V± are known as the effective potentials. They are functions of r , the integrals of motion lz and 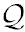 , and the parameters M and a. Actually, these quantities enter V only in the form of the dimensionless combinations r/M, lz/M,
, and the parameters M and a. Actually, these quantities enter V only in the form of the dimensionless combinations r/M, lz/M, 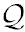 /M 2, and a/M.
/M 2, and a/M.
The motion of a particle with specific energy %E is possible only in the regions where either Ẽ ≥ V+ or Ẽ ≤ V−. The function for  remains invariant under transformations Ẽ → −Ẽ, lz → −lz relating the regions mentioned earlier. In the Schwarzschild geometry, the second region Ẽ ≤ V− is excluded, since, in the exterior of the black hole, Ẽ ≥ 0 and V− < 0. The limiting values of the effective potentials V± at infinity and at the horizon respectively are:
remains invariant under transformations Ẽ → −Ẽ, lz → −lz relating the regions mentioned earlier. In the Schwarzschild geometry, the second region Ẽ ≤ V− is excluded, since, in the exterior of the black hole, Ẽ ≥ 0 and V− < 0. The limiting values of the effective potentials V± at infinity and at the horizon respectively are:
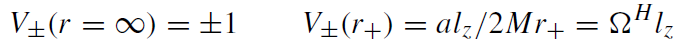 (1.16)
(1.16)
where ΩH is the angular velocity of the black hole. The effective potentials for non-rotating and rapidly rotating black holes are shown in figure 1.1.
1.5 Motion in the θ-direction
Let us consider the properties of the function Θ which determines the motion of a particle in the θ-direction. Since Θ ≥ 0 the finite motion with Ẽ2 < 1 is possible only if 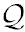 ≥ 0. The orbit is characterized by the value
≥ 0. The orbit is characterized by the value 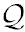 = 0 if and only if it is restricted to the equatorial plane. Non-equatorial finite orbits with θ = constant do not exist in the Kerr metric.
= 0 if and only if it is restricted to the equatorial plane. Non-equatorial finite orbits with θ = constant do not exist in the Kerr metric.
For 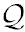 = 0, Θ is positive only if Ẽ2 > 1. The turning points ±θ0 in the θ-direction are defined by the equation
= 0, Θ is positive only if Ẽ2 > 1. The turning points ±θ0 in the θ-direction are defined by the equation
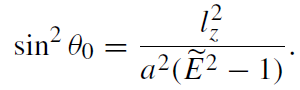 (1.17)
(1.17)
This equation implies that |lz| ≤ a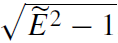 . Since in this case all the coefficients which enter
. Since in this case all the coefficients which enter  are non-negative, there are no turning points in r. The corresponding motion is infinite. It starts either at infinity and ends at the black hole horizon, or it starts near the black hole horizon and ends at infinity.
are non-negative, there are no turning points in r. The corresponding motion is infinite. It starts either at infinity and ends at the black hole horizon, or it starts near the black hole horizon and ends at infinity.
For 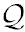 ≥ 0, there exist both finite as well as infinite trajectories. They intersect the equatorial plane or (for
≥ 0, there exist both finite as well as infinite trajectories. They intersect the equatorial plane or (for 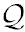 = 0 and Ẽ2 < 1) are entirely situated in it. The particles with
= 0 and Ẽ2 < 1) are entirely situated in it. The particles with 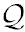 < 0 never cross the equatorial plane and move between two surfaces θ = θ+ and θ = θ− .
< 0 never cross the equatorial plane and move between two surfaces θ = θ+ and θ = θ− .
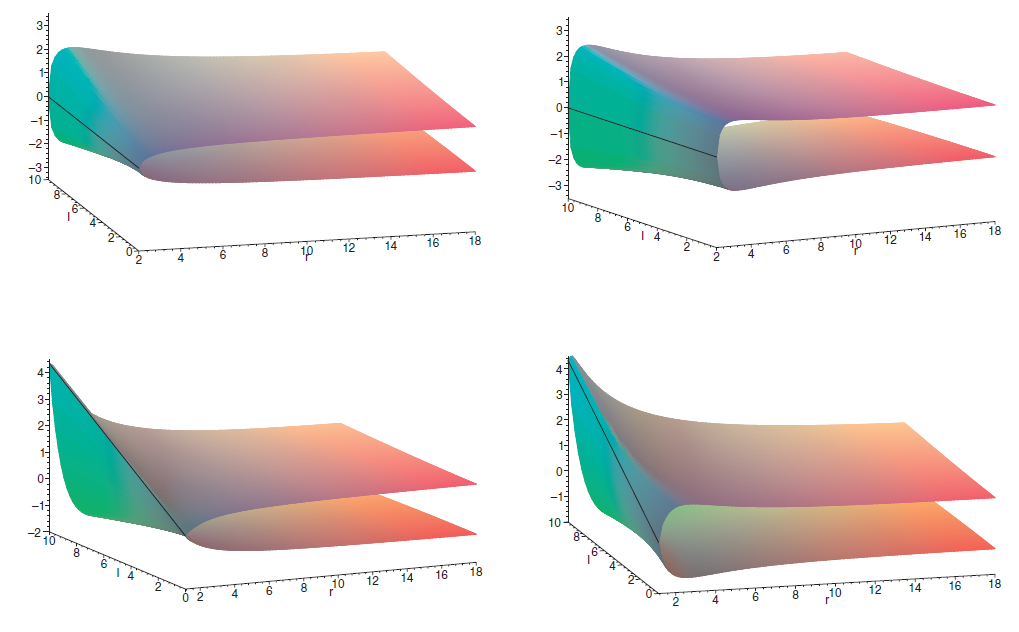
Figure 1.1. Effective potentials V± for the Kerr metric. The upper plots are for a = 0 (Q = 0 left and Q = 40 right); the lower ones are for a = 0.99 (Q = 0 left and Q = 40 right).
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















