Equation(i) satisfies the energy principle
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 203
29-1-2017
1642
Equation(i) satisfies the energy principle
(i)
By the ‘energy principle’ we understand the property that all energy of the self-gravitating system serves as source for the gravitational field. In this appendix, we wish to prove that (i) indeed satisfies this principle. For the uniqueness argument.
Given a matter distribution ρ immersed in its own gravitational potential φ, suppose we redistribute the matter within a bounded region of space by actively dragging it along the flow lines of a vector field 
which vanishes outside some bounded region. The rate of change, δρ, of the matter distribution is then determined through δρ dV = −L
(ρ dV) = −
· (
ρ) dV, where L
is the Lie derivative with respect to 
and dV is the standard spatial volume element. Note that the latter also needs to be differentiated along 
, resulting in L
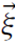dV = 
· 
. Hence we have δρ = −
· (
ρ). The rate of work done to the system during this process is
(1.1)
where the integration by parts does not lead to surface terms due to vanishing outside a bounded region. Equation (1.1) is still completely general, that is, independent of the field equation for φ. The field equation comes in when we assume that the process of redistribution is carried out adiabatically, which means that at each stage during the process φ satisfies its field equation with the instantaneous matter distribution. Our claim will be proven if under the hypothesis that φ we can show that δA = c2δMG, where MG is defined and represents the total gravitating energy according to the field equation. Setting 
= ψ and using the more convenient, we have
(1.2)
Now, the fall-off condition for r → ∞implies that 
ψ falls off as fast as 1/r2 and δψ as 1/r . Hence the second term in the last line of (1.2) does not contribute so that we may reverse its sign. This leads to
(1.3)
which proves the claim.
الاكثر قراءة في الثقوب السوداء
اخر الاخبار
اخبار العتبة العباسية المقدسة
