


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 29-1-2021
Date: 20-1-2021
Date: 9-3-2016
|
The laser equations in a resonator
As we know, in general laser processes take place within a resonator. It is defined with respect to the laser by the mirrors mounted at the endfaces of the laser material or by externally mounted mirrors. First let us consider the electric or electro-magnetic field in vacuum and the one-dimensional case (compare fig. 1.1). Let us assume that the conductivity of the mirrors is infinite. In such a case the tangential component of the electric field strength must vanish on the mirrors. This boundary condition is fulfilled by the electric field if it has nodes on the mirrors. In this case the electric field strength can be represented by
 (1.1)
(1.1)
Here k is given by mπ/ L, where L is the distance between the mirrors; m is an arbitrary integer. Thus in the resonator a set of different modes can develop. In the following we shall free ourselves from the specific form of the standing wave (1.1) and we shall denote the spatial part of the wave function by uλ(x). In the special case just considered u, has the form
 (1.2)
(1.2)
where e, is the unit vector in the direction of the field polarization, i.e. it is parallel to the electric field strength. N is a normalization factor and the spatial variation of uλ is described by the sine-function as in (1.1). But now we may also assume that uλ describes a three-dimensional configuration of the electric field, for instance waves which, so to speak, do not run parallel to the laser axis. The electric field strength which may be a general function of space and time can be represented by a superposition of such

Fig. 1.1. The electric field strength E(x) between two mirrors separated by the distance L.
standing waves uλ(x):
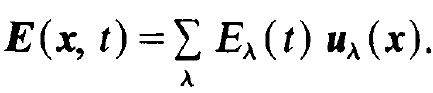 (1.3)
(1.3)
In it Eλ(t) are time dependent amplitudes. In the following we shall assume that the functions uλ of the individual modes obey a wave equation of the form
 (1.4)
(1.4)
As is shown in resonator theory, the functions uλ obey an orthogonality relation
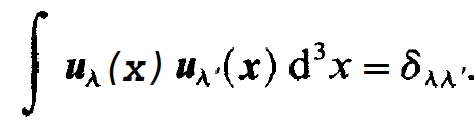 (1.5)
(1.5)
Because a laser resonator has open sides, the relations (1.5) are valid only approximately. We shall not discuss this question in more detail here, however. Our goal will rather be to derive equations for the field amplitudes Eλ(t). Our starting point is again the wave equation for the electric field strength which we briefly recall
 (1.6)
(1.6)
We insert (1.3) into it and use the relation (1.4) so that we may replace the spatial derivatives by a multiplication by -⍵2λ/c2. Then we multiply the resulting equation by uλ and integrate over the volume of the resonator. By means of the orthogonality relation (1.5) we obtain
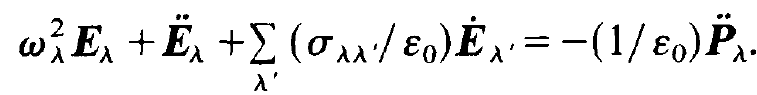 (1.7)
(1.7)
In it we have used μ0c2 = 1/ε0 and the abbreviation
 (1.8)
(1.8)
As we may recall, a is the electric conductivity of the material. If the material possesses a homogeneous conductivity we may pull a in front of the integral and may use again the orthogonality relation (1.5). If the conductivity varies spatially, for instance if it is concentrated in the mirrors, we must at least in principle be aware of the fact that also such σλλʹ ma y differ from 0 for A ≠ λ. Because this question leads to rather subtle discussions we shall not follow up this problem now but shall come back to it on later occasions. Finally we have to explain Pλ which occurs on the r.h.s. of (1.7). This is given by
 (1.9)
(1.9)
If we consider the decomposition (1.3) into the u's as Fourier decomposition, Pλ is nothing but a Fourier component of the polarization, P. In order to establish the relation of Pλ with the microscopic representation of the polarization, i.e. the individual dipole moments, we recall that the polarization P is related to the individual dipole moments pμ by
 (1.10)
(1.10)
Inserting (1.9) in (1.10) and recalling the property of the 8-function, we may immediately evaluate (1.9) and obtain
 (1.11)
(1.11)
So far we have transformed the equation for the electric field strength E into equations for the individual amplitudes Eλ(t). We now do the same for the matter equations. This means only some writing because in eqs. (i) and (ii) we have merely to replace on the r.h.s. E(xμ, t ) by the corresponding decomposition (1.3). We immediately obtain
 (1.12)
(1.12)
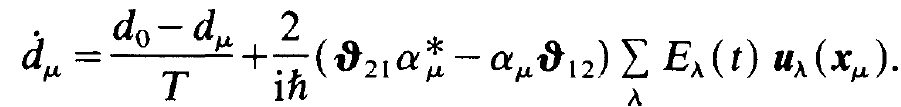 (1.13)
(1.13)
Eqs. (1.7), (1.12) and (1.13) represent a good starting point for the treatment of laser processes. In many cases these equations can be still considerably simplified, however, by introducing two approximations which in general are well founded.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|