
Rayleigh Scattering
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 77
الجزء والصفحة:
part 2 , p 77
 19-8-2016
19-8-2016
 2036
2036
Rayleigh Scattering
Rayleigh scattering is the elastic scattering of photons. Assume there is a matrix element M(k, k') which describes the scattering from k to k'. It has the dimensions of J m3.
a) Derive an expression for the differential cross section dσ/dΩ for Rayleigh scattering. Ignore the photon polarization.
b) Assume the specific form for the matrix element
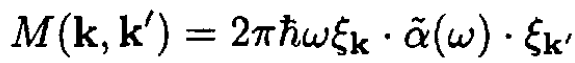 (i)
(i)
where  is the polarizability tensor and ξk are the polarization vectors of the photons. What is the result if the initial photons are unpolarized and the final photon polarizations are summed over? Assume the polarizability is isotropic:
is the polarizability tensor and ξk are the polarization vectors of the photons. What is the result if the initial photons are unpolarized and the final photon polarizations are summed over? Assume the polarizability is isotropic: 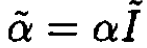 where Ĩ is the unit tensor.
where Ĩ is the unit tensor.
SOLUTION
a) The formula for the total cross section σ is
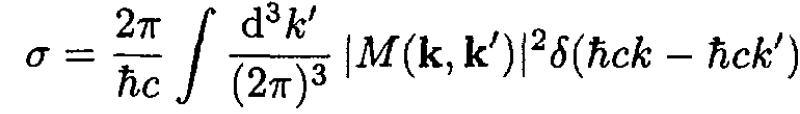 (1)
(1)
We write d3k' = k'2 dk' dΩ', where Ω' is the solid angle. The differential cross section is obtained by taking a functional derivative with respect to dΩ'. There remains only the dk' integral, which is eliminated by the delta function for energy conservation:
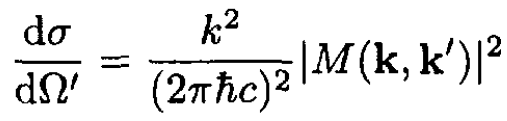 (2)
(2)
where the vector k' differs from k only in direction.
b) With the assigned choice of the matrix element we write our differential cross section as
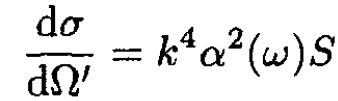 (3)
(3)
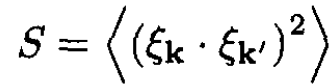 (4)
(4)
where the factor S is the average over initial polarizations and the sum over final polarizations. There are two possible polarizations, and both are perpendicular to the direction of the photon. These averages take the form
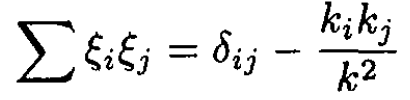 (5)
(5)
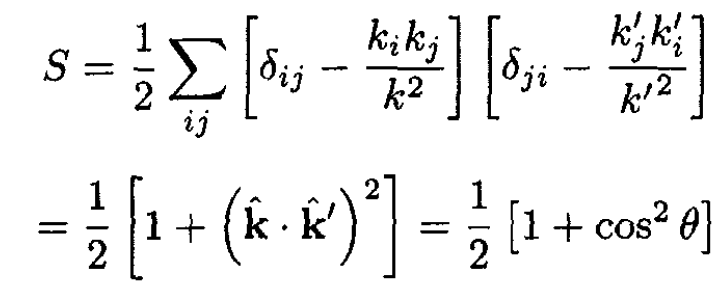 (6)
(6)
The factor 1/2 is from the average over initial polarization. The angle θ is between the directions of k and k'.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


