Superconducting Frame in Magnetic Field
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 76
11-8-2016
2516
Superconducting Frame in Magnetic Field
A superconducting square rigid frame of mass m, inductance L, and side a is cooled down (in a magnetic field) to a temperature below the critical temperature. The frame is kept horizontal (parallel to the x-y plane) and constrained to move in the z direction in a non-uniform but constant
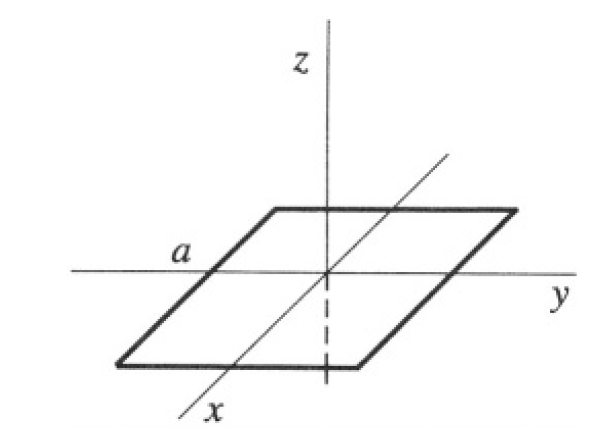
Figure 1.1
magnetic field described by a vector potential A = (-B0 y, αxz, 0) and a uniform gravitational field given by the acceleration g. The thickness of the frame is much smaller than a (see Figure 1.1). Initially, the frame is at rest, with its center coinciding with the origin. Find the equations of motion of the frame and solve for the position of the frame as a function of time.
SOLUTION
Find the magnetic field from the vector potential
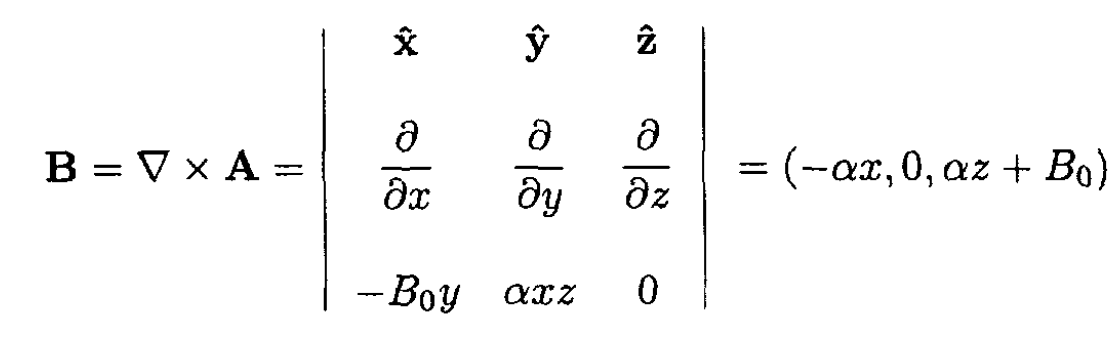
The magnetic flux Φ through the surface of the superconducting frame is constant (see Figure 1.2). Φ is composed of the flux from the external
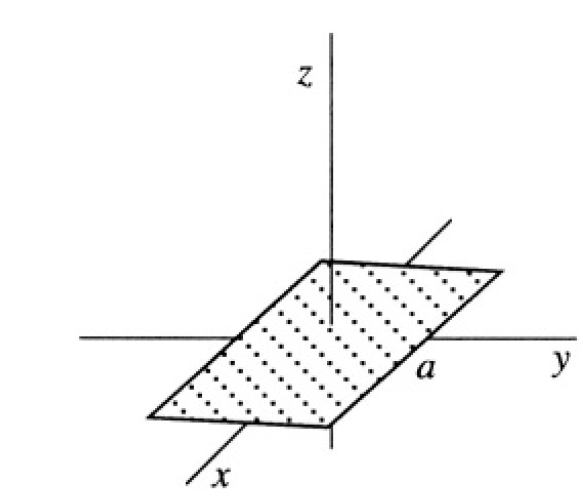
Figure 1.2
magnetic field Φe and the flux Φi produced by the current I flowing in the frame:
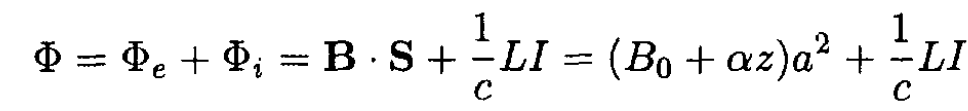
At t = 0, z = 0 and Φ = Φ0 = B0a2. At later times,
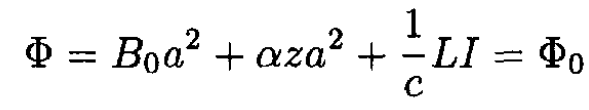
So for the current we have
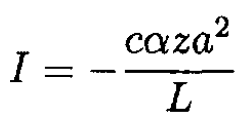
The force on the frame due to the interaction with the magnetic field is given by the general formula
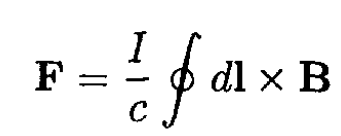
In this problem, due to the physical constraint, we need only the component in the z direction
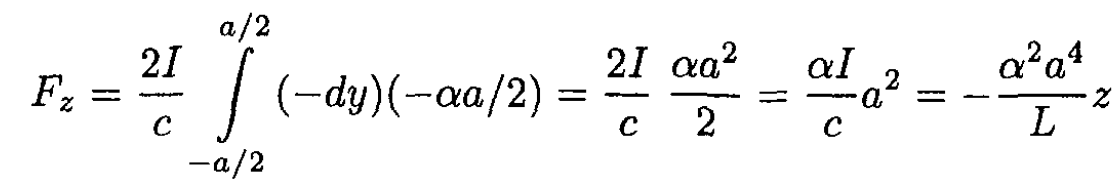
Therefore, the equation of motion becomes
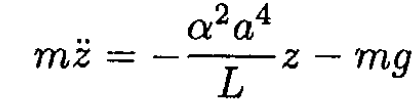
or
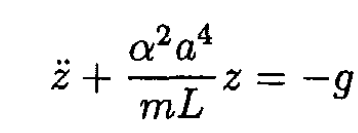
This equation describes oscillatory motion with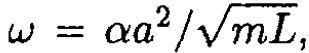 
and the solution is
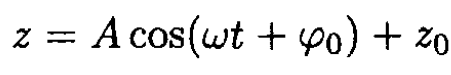
where
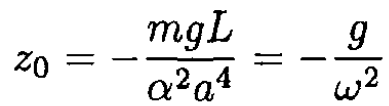
From the initial conditions z(0) = 0 and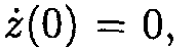 
we find that A = -z0 and φ0 = 0. The complete solution for the position of the frame along the z-axis at time t is
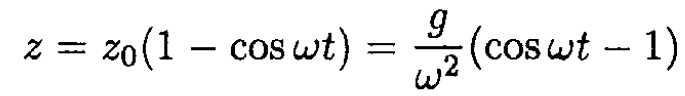
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
