
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Helium Atom
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 2 , p 65
18-8-2016
1667
Helium Atom
Do a variational calculation to estimate the ground state energy of the electrons in the helium atom. The Hamiltonian for two electrons, assuming the nucleus is fixed, is
 (i)
(i)
Assume a wave function of the form
 (ii)
(ii)
where a0 is the Bohr radius, α is the variational parameter, and χs is the spin state of the two electrons.
SOLUTION
In the ground state of the two-electron system, both orbitals are in 1s states. So the spin state must be a singlet χs with S = 0. The spin plays no role in the minimization procedure, except for causing the orbital state to have even parity under the interchange of spatial coordinates. The two-electron wave function can be written as the product of the two orbital parts times the spin part:
 (1)
(1)
 (2)
(2)
where a0 is the Bohr radius and α is the variational parameter. The orbitals ѱ(r) are normalized to unity. Each electron has kinetic (K) and potential (U) energy terms which can be evaluated:
 (3)
(3)
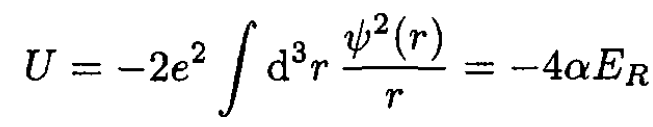 (4)
(4)
where ER = 13.6 eV is the Rydberg energy. The difficult integral is that due to the electron–electron interaction, which we call V:
 (5)
(5)
First we must do the angular integral over the denominator. If rm is the larger of r1 and r2 then the integral over a 4π solid angle gives
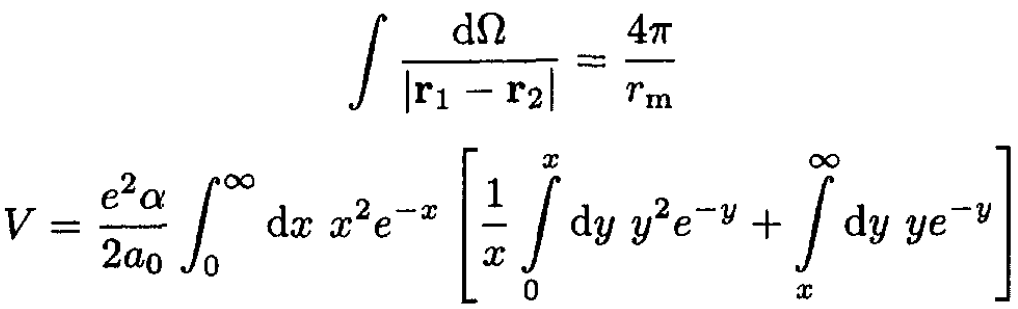 (6)
(6)
In the second integral we have set x = 2αr1/a0 and y = 2αr2/a0, which makes the integrals dimensionless. Then we have split the y-integral into two parts, depending on whether y is smaller or greater than x. The first has a factor 1/x from the angular integrals, and the second has a factor 1/y. One can exchange the order of integration in one of the integrals and demonstrate that it is identical to the other. We evaluate only one and multiply the result by 2:
 (7)
(7)
 (8)
(8)
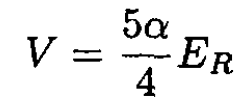 (9)
(9)
This completes the integrals. The total ground state energy E(α) in Rydbergs is
 (10)
(10)
We find the minimum energy by varying α. Denote by α0 the value of α at which E(α) is a minimum. Setting to zero the derivative of E(α) with respect to α yields the result α0= 27/16. The ground state energy is
 (11)
(11)
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















