
Attractive Delta Function in 3D
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 78
الجزء والصفحة:
part 2 , p 78
 14-8-2016
14-8-2016
 2057
2057
Attractive Delta Function in 3D
A particle moves in three dimensions. The only potential is an attractive delta function at r = a of the form
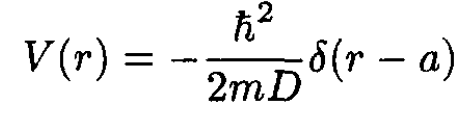 (i)
(i)
where D is a parameter which determines the strength of the potential.
a) What are the matching conditions at r = a for the wave function and its derivative?
b) For what values of D do bound states exist for s-wave (ℓ = 0).
SOLUTION
a) The amplitude of the wave function is continuous at the point r = a of the delta function. For the derivative we first note that the eigenfunctions are written in terms of a radial function R(r) and angular functions:
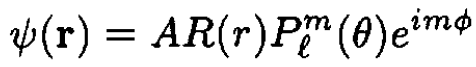 (1)
(1)
Since the delta function is only for the radial variable r, only the function R(r) has a discontinuous slope. From the radial part of the kinetic energy operator we integrate from r = a- to r = a+:
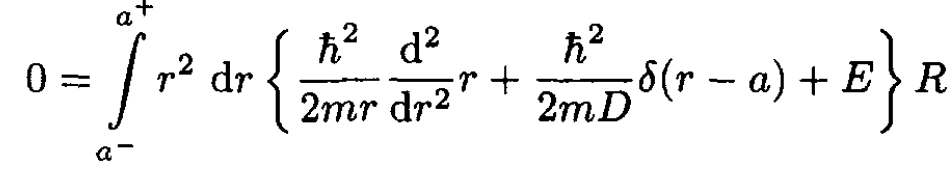 (2)
(2)
 (3)
(3)
This formula is used to match the slopes at r = a.
b) In order to find bound states, we assume that the particle has an energy given by E = -h2α2/2m, where α needs to be determined by an eigenvalue equation. The eigenfunctions are combinations of exp (±α)/r. In order to be zero at r = 0 and to vanish at infinity, we must choose the form
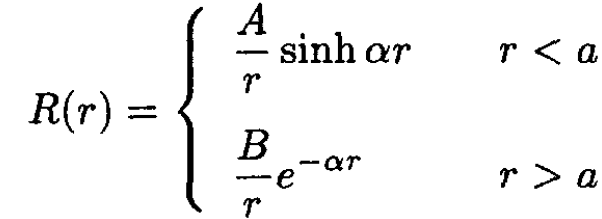 (4)
(4)
We match the values of R(r) at r = a. We match the derivative, using the results of part (a):
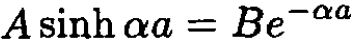 (5)
(5)
 (6)
(6)
We eliminate the constants A and B and obtain the eigenvalue equation for α, which we proceed to simplify:
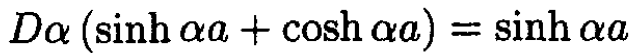 (7)
(7)
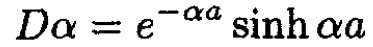 (8)
(8)
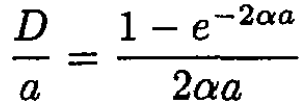 (9)
(9)
This is the eigenvalue equation which determines α as a function of parameters such as a, D, m etc. In order to find the range of allowed values of D for bound states, we examine αa → 0. The right-hand side of (9) goes to 1, which is its largest value. So, the constraint for the existence of bound states is
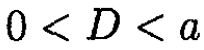 (10)
(10)
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


