Lifetime of Classical Atom
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 69
9-8-2016
2147
Lifetime of Classical Atom
At a time t = 0, the electron orbits a classical hydrogen atom at a radius a0 equal to the first Bohr radius. Derive an expression for the time it takes for the radius to decrease to zero due to radiation. Assume that the energy loss per revolution is small compared to the total energy of the atom.
SOLUTION
If the energy loss per revolution is small compared to the total energy of the electron in the atom, we can write
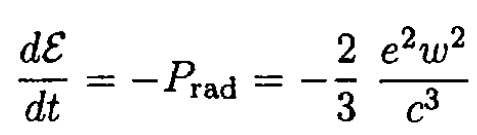(1)
where ω is the acceleration of the electron and Prad is the total radiated power. Using our assumption, we can approximate the orbit of the electron (which is a spiral) by a circle for each revolution of radius r = r(t). The acceleration is due to the Coulomb force
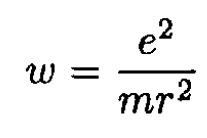(2)
On the other hand, using |ε| = |U|/2 (U is the potential energy of a particle moving in a circle in a 1/r2 field) we have
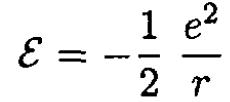(3)
Substituting (2) and (3) into (1) gives
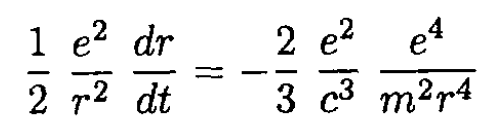(4)
or
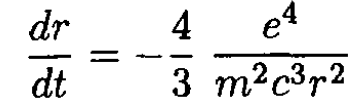(5)
Integrating (5) yields
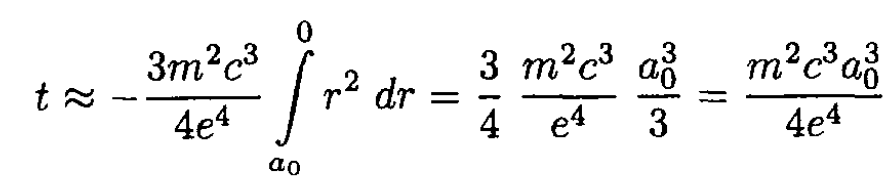
So
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
