
Concentric Spherical Capacitor
 المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 48
الجزء والصفحة:
part 1 , p 48
 8-8-2016
8-8-2016
 2193
2193
Concentric Spherical Capacitor
Consider two concentric metal spheres of finite thickness in a vacuum. The inner sphere has radii a1 < a2. The outer sphere has b1 < b2 (see Figure 1.1).

Figure 1.1
a) A charge Q1 is put on the inner sphere and a charge Q2 on the outer sphere. Find the charge density on each of the four surfaces. If Q2 = -Q1 what is the mutual capacitance of the system?
b) If the space between the spheres is filled with insulating material of dielectric constant ε1, what are the surface charge densities and polarization surface charge densities for arbitrary Q1 and Q2 and the mutual capacitance for Q2 = -Q1.
SOLUTION
a) By using Gauss’s theorem and the fact that charges rearrange themselves so as to yield a zero electric field inside the conductors, we infer that all of Q1 will reside on surface 2 of the inner sphere, -Q1 on surface 3 of the outer sphere (no field in the interior of the outer sphere), and Q1 + Q2 on surface 4 of the outer sphere (see Figure 1.2). The surface charge
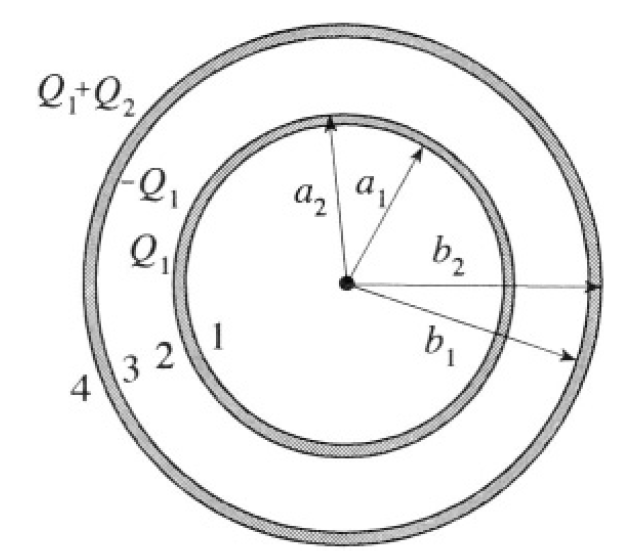
Figure 1.2
densities are straightforward to calculate as the charge divided by surface area:
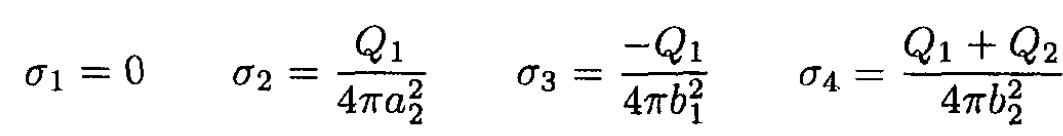
If Q2 = -Q1, there is no charge on the external shell, simply Q1 on surface 2 and –Q1 on surface 3. The mutual capacitance may be calculated from ∆VC = Q1, where ∆V is the difference in electric potential between the spherical shells. Again using Gauss’s theorem to calculate the magnitude E of the electric field between the shells, we have
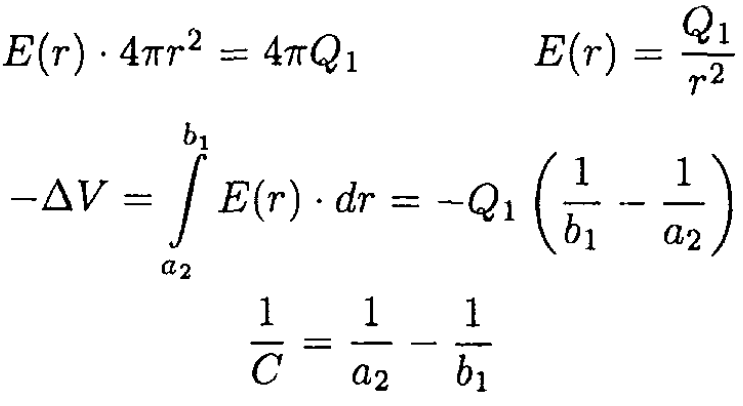
b) The D field behaves like the E field before:
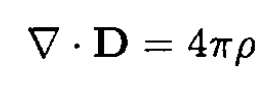
so, between the spheres
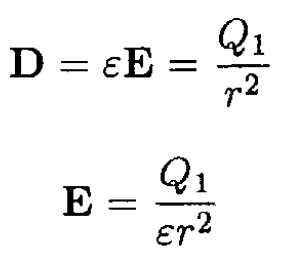
The real and polarization surface charge densities on surface 1 are still zero, and on surface 2, we find
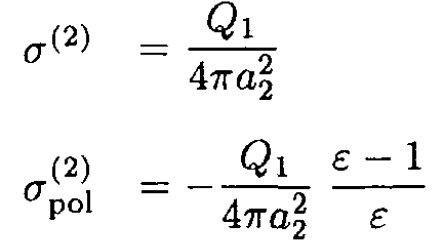
Likewise, on the third and fourth surfaces,
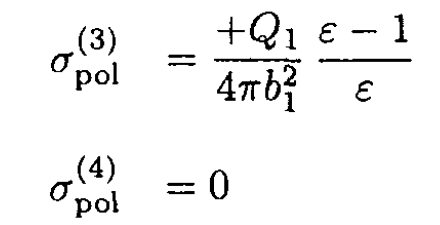
Finally, the capacitance may be found:
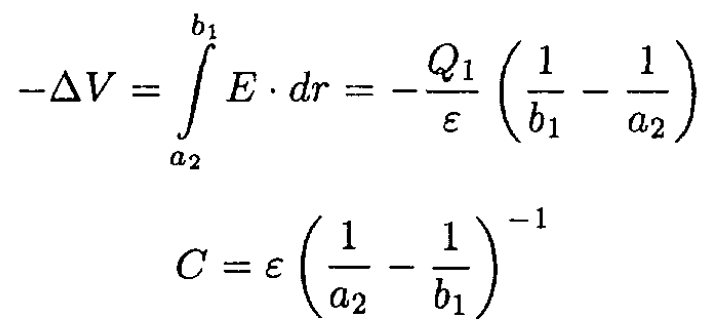
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


